「三角関数」の版間の差分
パンの袋を留めるやつ (会話) による ID:50479707 の版を取り消し - 本項で扱うには少し特殊過ぎる。 |
|||
| (100人の利用者による、間の382版が非表示) | |||
| 1行目: | 1行目: | ||
{{redirect|タンジェント|バンド|タンジェント (バンド)}} |
|||
'''三角関数'''(さんかくかんすう、{{lang-en-short|trigonometric function}})とは、平面[[三角法]]における、[[角]]の大きさと[[線分]]の長さの関係を明らかにする[[関数_(数学)|関数]]の族および、それらを拡張して得られる関数の総称である。 |
|||
{{混同|三角数}} |
|||
{{色}} |
|||
'''三角関数'''(さんかくかんすう、{{lang-en-short|trigonometric function}})とは、平面[[三角法]]における、[[角度]]の大きさと[[線分]]の長さの関係を記述する[[関数_(数学)|関数]]の[[族 (数学)|族]]、およびそれらを拡張して得られる関数の総称である。鋭角を扱う場合、三角関数の値は対応する[[直角三角形]]の二辺の長さの比('''三角比''')である。三角法に由来する'''三角関数'''という呼び名のほかに、[[単位円]]を用いた定義に由来する'''円関数'''(えんかんすう、{{lang|en|circular function}})という呼び名がある。 |
|||
[[ファイル:Circle-trig6.svg|300px|thumb|right|単位円による、6つの三角関数が表す長さ。<hr>{{table2|class=none|cols=2|style=font-weight:bold| {{colorbox|#FF0000| }} 正弦 {{math|sin}} | {{colorbox|#0000FF| }} 余弦 {{math|cos}} | {{colorbox|#D3B58D| }} 正接 {{math|tan}} | {{colorbox|#FF8D00| }} 余接 {{math|cot}} | {{colorbox|#A7D0D0| }} 正割 {{math|sec}} | {{colorbox|#FFC1CC| }} 余割 {{math|csc (cosec)}} }}]] |
|||
三角関数には以下の6つがある。なお、正弦、余弦、正接の3つのみを指して三角関数と呼ぶ場合もある。 |
|||
* '''正弦(せいげん)'''、{{math|sin}}({{en|<u>sin</u>e}}) |
|||
* '''余弦(よげん)'''、{{math|cos}}({{en|<u>cos</u>ine}}) |
|||
* '''正接(せいせつ)'''、{{math|tan}}({{en|<u>tan</u>gent}}) |
|||
* '''正割(せいかつ)'''、{{math|sec}}({{en|<u>sec</u>ant}}) |
|||
* '''余割(よかつ)'''、{{math|csc,cosec}}({{en|<u>c</u>o<u>s</u>e<u>c</u>ant}}) |
|||
* '''余接(よせつ)'''、{{math|cot}}({{en|<u>cot</u>angent}}) |
|||
特に {{math|sin, cos}} は[[幾何学]]的にも[[解析学]]的にも良い性質をもっているので、様々な分野で用いられる。例えば、[[波動|波]]や[[信号 (電気工学)|信号]]などは正弦関数と余弦関数とを組み合わせて表現することができる。この事実は[[フーリエ級数]]および[[フーリエ変換]]の理論として知られ、音声などの信号の合成や解析の手段として利用されている。[[空間ベクトル|ベクトル]]の[[クロス積]]や[[内積]]は正弦関数および余弦関数を用いて表すことができ、ベクトルを図形に対応づけることができる。初等的には、三角関数は[[実数]]を[[媒介変数|変数]]とする1変数関数として定義される。三角関数の変数に対応するものとしては、図形のなす角度や、物体の回転角、波や信号のような周期的なものにおける[[位相]]などが挙げられる。 |
|||
三角関数に用いられる独特な記法として、三角関数の[[冪乗]]と逆関数に関するものがある。通常、関数 {{math|''f''(''x'')}} の累乗は {{math|(''f''(''x''))<sup>2</sup> {{=}} ''f''(''x'')・''f''(''x'')}} や {{math|(''f''(''x''))<sup>−1</sup> {{=}} 1/''f''(''x'')}} のように書くが、三角関数の累乗は {{math|sin<sup>2</sup>''x''}} のように書かれることが多い。[[逆三角関数]]については通常の記法 ({{math|''f''<sup>−1</sup>(''x'')}}) と同じく、{{math|sin<sup>−1</sup>''x''}} などと表す(この文脈では、三角関数の[[逆数]]は分数を用いて {{math|{{sfrac|1|sin ''x''}}}} または {{math|(sin ''x'')<sup>−1</sup>}} のように表される)。文献または著者によっては、通常の記法と三角関数に対する特殊な記法との混同を避けるため、三角関数の累乗を通常の関数と同様にすることがある。また、三角関数の逆関数として {{math|−1}} を添え字にする代わりに関数の頭に {{math|arc}} を付けることがある(たとえば {{math|sin}} の逆関数として {{math|sin<sup>−1</sup>}} の代わりに {{math|arcsin}} を用いる。{{math|Arc}} を付けて {{math|Arcsin}} と表すこともある)。 |
|||
三角関数に似た性質をもつ関数として、[[指数関数]]、[[双曲線関数]]、[[ベッセル関数]]などがある。また、三角関数を利用して定義される関数としてしばしば応用されるものに[[sinc関数]]がある。 |
|||
== 定義 == |
== 定義 == |
||
=== 直角三角形による |
=== 直角三角形によるもの === |
||
[[ファイル:Trigonometry triangle.svg|thumb|250px|∠C を直角とする直角三角形ABC]] |
[[ファイル:Trigonometry triangle.svg|thumb|250px|{{math|∠C}} を直角とする直角三角形ABC<br/>{{colorbox|#0000FF| }} 斜辺AB = h (hypotenuse)<br/>{{colorbox|#FF0000| }} 対辺BC = a (opposite side)<br/>{{colorbox|#008100| }} 底辺AC = b (adjacent side、隣辺)]] |
||
[[直角三角形]]において、1つの鋭角の大きさが決まれば、[[三角形]]の内角の和は180°であることから他の1つの鋭角の大きさも決まり、3辺の比も決まる。ゆえに、角度に対して辺比の値を与える関数を考えることができる。 |
[[直角三角形]]において、1 つの鋭角の大きさが決まれば、[[三角形]]の内角の和は {{math|180°}}であることから他の 1 つの鋭角の大きさも決まり、3 辺の比も決まる。ゆえに、角度に対して辺比(三角比)の値を与える関数を考えることができる。 |
||
∠C を直角とする直角三角形ABC において、AB = ''h'', BC = ''a'', CA = ''b'' と |
{{math|∠C}} を直角とする直角三角形 ABC において、斜辺AB、{{math|∠A}} の[[対辺]]BC、底辺(隣辺)CA の辺の長さをそれぞれ {{math|AB {{=}} ''h'', BC {{=}} ''a'', CA {{=}} ''b''}} と表す(図を参照)。{{math|∠A {{=}} ''θ''}} に対して三角形の辺の比 {{math|''h'' : ''a'' : ''b''}} が決まることから、 |
||
:<math>\ |
:<math>\begin{align} |
||
\sin \theta &= \frac{a}{h} \\ |
|||
\cos \theta &= \frac{b}{h} \\ |
|||
\tan \theta &= \frac{a}{b} = \frac{\sin \theta}{\cos \theta} \\ |
|||
\sec \theta &= \frac{h}{b} = \frac{1} |
|||
{\cos \theta} \\ |
|||
\operatorname{cosec} \theta &= \csc \theta = \frac{h}{a} = \frac{1} |
|||
{\sin \theta} \\ |
|||
という6つの値が定まる。それぞれ'''正弦'''(sine(サイン))・'''余弦'''(cosine(コサイン))・'''正接'''(tangent(タンジェント))・'''余割'''(cosecant(コセカント))・'''正割'''(secant(セカント))・'''余接'''(cotangent(コタンジェント))と呼び、まとめて'''三角比'''と呼ばれる。ただし cosec は長いので csc と略記することも多い。また、余弦、余割、余接は余角(角を90°から引いた角)のそれぞれ正弦、正割、正接に等しい。三角比は平面[[三角法]]に用いられ、巨大な物の大きさや遠方までの距離を計算する際の便利な道具となる。角度 ''θ'' の単位は、通常[[度 (角度)|度]]または[[ラジアン]]である。 |
|||
\cot \theta &= \frac{b}{a} = \frac{1} |
|||
{\tan \theta} |
|||
\end{align}</math> |
|||
という 6 つの値が定まる。それぞれ{{nobr|'''正弦:sin'''({{en|<u>sin</u>e;}} サイン)、}}{{nobr|'''余弦:cos'''({{en|<u>cos</u>ine;}} コサイン)、}}{{nobr|'''正接:tan'''({{en|<u>tan</u>gent;}} タンジェント)、}}{{nobr|'''正割:sec'''({{en|<u>sec</u>ant;}} セカント)、}}{{nobr|'''余割:cosec'''({{en|<u>cosec</u>ant;}} コセカント)、}}{{nobr|'''余接:cot'''({{en|<u>cot</u>angent;}} コタンジェント)}}と呼び、まとめて'''三角比'''と呼ばれる。ただし {{math|cosec}} は長いので {{math|csc}} と略記することも多い。 |
|||
{| class="wikitable" style="text-align:center" |
|||
|+ style="text-align:left; white-space:nowrap;"|三角関数の和名と定義 |
|||
! |
|||
!colspan="2" style="width:6em"|[[弦_(数学)|_弦]] |
|||
!colspan="2" style="width:6em"|[[接線|_接]] |
|||
!colspan="2" style="width:6em"|[[割線|_割]] |
|||
|rowspan="4" style="text-align:left"|∠C を直角とする直角三角形 ABC<br/> ''h'' = 斜辺AB <br/> ''a'' = 対辺BC <br/> ''b'' = 底辺AC |
|||
|- |
|||
!正_ |
|||
|正弦<br/>(sin) ||<math>{a \over h}</math> |
|||
|正接<br/>(tan) ||<math>{a \over b}</math> |
|||
|正割<br/>(sec) ||<math>{h \over b}</math> |
|||
|- |
|||
!余_ |
|||
|余弦<br/>(cos) ||<math>{b \over h}</math> |
|||
|余接<br/>(cot) ||<math>{b \over a}</math> |
|||
|余割<br/>(csc) ||<math>{h \over a}</math> |
|||
|} |
|||
ある正角 {{math|∠A}} に対する余弦、余割、余接はその角 {{math|∠A}} の[[角度#角同士の関係による分類|余角]] {{en|(co-angle)}}に対する正弦、正割、正接として定義される。ここで余角とは「鋭角(正角)に対し合わせて直角となる角」を指し、この場合は 正角{{math|∠A}}に対する余角は{{math|∠B}}となる。 |
|||
:<math>\begin{align} |
|||
\cos \theta &= \sin \left(90^\circ - \theta \right) = \sin \left(\frac{\pi}{2} - \theta \right)\\ |
|||
\csc \theta &= \sec \left(90^\circ - \theta \right) = \sec \left(\frac{\pi}{2} - \theta \right)\\ |
|||
\cot \theta &= \tan \left(90^\circ - \theta \right) = \tan \left(\frac{\pi}{2} - \theta \right) |
|||
\end{align}</math> |
|||
三角比は平面[[三角法]]に用いられ、巨大な物の大きさや遠方までの距離を計算する際の便利な道具となる。角度 {{mvar|θ}} の単位は、通常[[度 (角度)|度]]または[[ラジアン]]である。 |
|||
三角比、すなわち三角関数の直角三角形を用いた定義は、直角三角形の鋭角に対して定義されるため、その定義域は {{math|''θ''}} が 0° から 90° まで(0 から π / 2 まで)の範囲に限られる。また、{{math|''θ'' {{=}} 90° ({{=}} π / 2)}} の場合 {{math|sec, tan}} が、{{math|''θ'' {{=}} 0°({{=}} 0)}} の場合 {{math|csc, cot}} がそれぞれ定義されない。これは分母となる辺の比の大きさが 0 になるため[[ゼロ除算]]が発生し、その除算自体が数学的に定義されないからである。一般の角度に対する三角関数を得るためには、三角関数について成り立つ何らかの定理を指針として、定義の拡張を行う必要がある。[[#単位円によるもの|単位円による定義]]は初等幾何学におけるそのような拡張の例である。他に同等な方法として、[[正弦定理]]や[[余弦定理]]を用いる方法などがある。 |
|||
=== 単位円による定義 === |
|||
[[ファイル:Circle-trig6.svg|300px|thumb|right|単位円による、6つの三角関数が表す長さ]] |
|||
実数 ''t'' に対して、2次元[[ユークリッド空間]] '''R'''{{sup|2}} における[[単位円]] ''x''{{sup|2}} + ''y''{{sup|2}} = 1 上の点P(''x'', ''y'') を ∠''x''OP = ''t''(反時計回りを正の向きとする)を満たすように取り、 |
|||
:<math>\sin t=y</math> |
|||
:<math>\cos t=x</math> |
|||
:<math>\tan t=\frac{y}{x} =\frac{\sin t}{\cos t}</math> |
|||
と定義する。順に'''正弦関数'''(sine; サイン)・'''余弦関数'''(cosine; コサイン)・'''正接関数'''(tangent; タンジェント)と呼び、これらを総称して'''三角関数'''と呼ぶ。さらにこれらの逆数 |
|||
:<math>\csc t=\frac{1}{y} =\frac{1}{\sin t}</math> |
|||
:<math>\sec t=\frac{1}{x} =\frac{1}{\cos t}</math> |
|||
:<math>\cot t =\frac{x}{y} =\frac{1}{\tan t}</math> |
|||
を順に'''余割関数'''(cosecant; コセカント)・'''正割関数'''(secant; セカント)・'''余接関数'''(cotangent; コタンジェント)と呼び、これらを総称して'''割三角関数'''(かつさんかくかんすう)と呼ぶ。これらを含めて三角関数と呼ぶこともある。 |
|||
=== |
=== 単位円によるもの === |
||
[[File:TrigFunctionDiagram.svg|thumb|6種類の三角関数、単位円、{{math|1=θ = 0.7}}ラジアンの角度に対する直線の図。直線の色が変わる点3点を考えたとき、{{color|#A00|1}}、{{color|#00A|Sec(θ)}}、{{color|#0A0|Csc(θ)}}については原点から各点への線分の長さを表し、{{color|#A00|Sin(θ)}}、{{color|#00A|Tan(θ)}}、{{color|#0A0|1}} |
|||
角度、辺の長さといった幾何学的な概念に依存しないために、[[級数]]で定義することもできる。収束半径を求めることより、以下の級数は収束円上で収束する。 |
|||
は各点のy成分を表す。{{color|#A00|Cos(θ)}}、{{color|#00A|1}}、{{color|#0A0|Cot(θ)}}は各点の x 成分を表す。]] |
|||
2 次元[[ユークリッド空間]] {{math|'''R'''<sup>2</sup>}} における[[単位円]] {{math|{''x''(''t'')}<sup>2</sup> + {''y''(''t'')}<sup>2</sup> {{=}} 1}} 上の点を {{math|A {{=}} (''x''(''t''), ''y''(''t''))}} とする。反時計回りを正の向きとして、原点と円周を結ぶ線分 {{math|OA}} と {{mvar|x}} 軸のなす角の大きさ {{math|∠''x''OA}} を[[媒介変数]] {{mvar|t}} として選ぶ。このとき[[実数]]の変数 {{mvar|t}} に対する三角関数は以下のように定義される。 |
|||
:<math>\begin{align} |
|||
\sin t &= y\\ |
|||
\cos t &= x\\ |
|||
\tan t &= \frac{y}{x} = \frac{\sin t}{\cos t} |
|||
\end{align}</math> |
|||
これらは順に'''正弦関数''' {{en|(<u>sin</u>e function)}}、'''余弦関数''' {{en|(<u>cos</u>ine function)}}、'''正接関数'''{{en|(<u>tan</u>gent function)}} と呼ばれる。さらにこれらの[[逆数]]として以下の 3 つの関数が定義される。 |
|||
:<math>\begin{align} |
|||
\csc t &= \frac{1}{y} = \frac{1}{\sin t}\\ |
|||
\sec t &= \frac{1}{x} = \frac{1}{\cos t}\\ |
|||
\cot t &= \frac{x}{y} = \frac{1}{\tan t} |
|||
\end{align}</math> |
|||
これらは順に'''余割関数''' {{en|(<u>cosec</u>ant function)}}、'''正割関数''' {{en|(<u>sec</u>ant function)}}、'''余接関数''' {{en|(<u>cot</u>angent function)}} と呼ばれ、{{math|sin, cos, tan}} と合わせて'''三角関数'''と総称される。特に {{math|csc, sec, cot}} は'''割三角関数'''(かつさんかくかんすう)と呼ばれることがある。 |
|||
この定義は {{math|0 < ''t'' < π / 2}} の範囲では[[#直角三角形によるもの|直角三角形による定義]]と一致する。 |
|||
''z'' を複素数、''B{{sub|n}}'' を[[ベルヌーイ数]]、''E{{sub|n}}'' を[[オイラー数]]とする。 |
|||
:<math>\sin z=\sum^{\infin}_{n=0} \frac{(-1)^n}{(2n+1)!} z^{2n+1}\quad \text{for all} \ z</math> |
|||
:<math>\cos z=\sum^{\infin}_{n=0} \frac{(-1)^n}{(2n)!} z^{2n}\quad \text{for all} \ z</math> |
|||
:<math>\tan z=\sum^{\infin}_{n=1} \frac{ (-1)^n 2^{2n} (1-2^{2n}) B_{2n}}{(2n)!} z^{2n-1}\quad \text{for} \ |z|<\frac{\pi}{2}</math> |
|||
:<math>\csc z=\sum^{\infin}_{n=0} \frac{(-1)^n (2-2^{2n}) B_{2n}}{(2n)!} z^{2n-1}\quad \text{for} \ 0<|z|<\pi</math> |
|||
:<math>\sec z=\sum^{\infin}_{n=0} \frac{(-1)^n E_{2n}}{(2n)!} z^{2n} \quad \text{for} \ |z|<\frac{\pi}{2}</math> |
|||
:<math>\cot z=\sum^{\infin}_{n=0} \frac{(-1)^n 2^{2n} B_{2n}}{(2n)!} z^{2n-1}\quad \text{for} \ 0<|z|<\pi</math> |
|||
== |
=== 級数によるもの === |
||
角度、辺の長さといった幾何学的な概念への依存を避けるため、また[[定義域]]を[[複素数]]に拡張するために、[[級数]](他の定義を採用した三角関数の[[テイラー展開]]に一致する)を用いて定義することもできる。この定義は実数の範囲では単位円による定義と一致する。以下の級数は共に示される収束円内で収束する。 |
|||
{{main|{{仮リンク|三角関数の歴史|en|History of trigonometric functions}}}} |
|||
{{Seealso|円周率|円周率の歴史}} |
|||
* {{mvar|z}} を[[複素数]]、{{mvar|B<sub>n</sub>}} を[[ベルヌーイ数]]、{{mvar|E<sub>n</sub>}} を[[オイラー数]]とする。 |
|||
一定の半径の円における中心角に対する[[弦 (数学)|弦]]と[[弧 (幾何学)|弧]]の長さの関係は、[[測量]]や[[天文学]]の要請によって古代から研究されてきた。 |
|||
:<math>\begin{align} |
|||
\sin z &= \sum^{\infin}_{n=0} \frac{(-1)^n}{(2n+1)!} z^{2n+1}\quad \text{for all} \ z, \\ |
|||
\cos z &= \sum^{\infin}_{n=0} \frac{ \left(-1 \right)^n}{ \left(2n \right)!} z^{2n}\quad \text{for all} \ z, \\ |
|||
\tan z &= \sum^{\infin}_{n=1} \frac{ \left(-1 \right)^n 2^{2n} \left(1-2^{2n} \right) B_{2n}}{ \left(2n \right)!} z^{2n-1}\quad \text{for} \ |z| < \frac{\pi}{2}, \\ |
|||
\cot z &= \sum^{\infin}_{n=0} \frac{ \left(-1 \right)^n 2^{2n} B_{2n}}{ \left(2n \right)!} z^{2n-1}\quad \text{for} \ 0 < |z| < \pi, \\ |
|||
\sec z &= \sum^{\infin}_{n=0} \frac{ \left(-1 \right)^n E_{2n}}{ \left(2n \right)!} z^{2n} \quad \text{for} \ |z|<\frac{\pi}{2}, \\ |
|||
\csc z &= \sum^{\infin}_{n=0} \frac{ \left(-1 \right)^{n} \left(2-2^{2n}\right) B_{2n}}{ \left(2n \right)!} z^{2n-1}\quad \text{for} \ 0 < |z|< \pi. |
|||
\end{align}</math> |
|||
=== |
=== 微分方程式によるもの === |
||
古代ギリシャにおいて、円と球に基づく宇宙観に則った天文学研究から、[[ヒッパルコス]]により一定の半径の円における中心角に対する弦の長さが表にまとめられたもの(正弦表)が作られた。[[クラウディオス・プトレマイオス|プトレマイオス]]の『[[アルマゲスト]]』にも正弦表が記載されている。 |
|||
実関数 {{math|''f''(''x'')}} の二階線型[[常微分方程式]]の初期値問題 |
|||
=== 古代インド === |
|||
{{numBlk|:|<math>f''(x) = -f(x),\;f(0)=1,\;f'(0)=0</math>|{{equationRef|DE1|1}}}} |
|||
正弦表は後にインドに伝わり、弦の長さは半分でよいという考えから[[5世紀]]頃には半弦 ardha-jiva(つまり現在の sine の意味の正弦)の長さをより精確にまとめたものが作成された(『アールヤバタ』)。ardha は"半分" jiva は"弦"の意味で、当時のインドではこの半弦(現在の sine の意味の正弦)は単に jiva と略された。また、弦の長さを半分にして直角三角形を当てはめたことから派生して余角 (complementary angle) の考えが生まれ、“余角 (co-angle) の正弦 (sine)”という考えから余弦 (cosine) の考えが生まれた。余弦の値もこの頃に詳しく調べられている。(*co- は complementary の略で、補完的・補足的という意味の接頭語として用いる) |
|||
の解として {{math|cos''x''}} を定義し、{{math|sin''x''}} を {{math|−''d'' (cos''x'')/''dx''}} として定義できる<ref name="三角関数の研究" /><ref name="NaitoFourierLecture1999" />。上記の式を 1 階の連立常微分方程式に書き換えると、{{math|''g''(''x'') {{=}} ''f {{'}}''(''x'')}} として、 |
|||
{{numBlk|:|<math>\begin{cases} |
|||
f'(x) = g(x), \\ |
|||
g'(x) = -f(x) |
|||
\end{cases}</math>|{{equationRef|DE2|2}}}} |
|||
および初期条件 {{math|1=''f''(0) = 1, ''g''(0) = 0}} となる。 |
|||
=== |
=== 他の定義 === |
||
この他にも定積分による(逆三角関数を用いた)定義や複素平面の角の回転による定義などが知られている<ref name="三角関数の研究" />{{Sfn|黒田成俊|2002|pp=176-183}}{{Sfn|高木貞治|2010|pp=202-206}}{{Sfn|小平邦彦|2003|pp=95-105}}<ref name="三角関数と円周率" /><ref name="三角関数のさまざまな定義" />。 |
|||
[[8世紀]]頃イスラム帝国へ伝わったときに jaib(入り江)と変化した。10世紀の[[アッバース朝]]時代にシリアの数学者[[バッターニー|アル・バッターニ]]が正弦法の導入、コタンジェント表の計算、球面三角法([[球面幾何学]])の定理を提唱した。[[ブワイフ朝]]の[[バグダード]]の数学者[[アブル・ワファー]]が[[タンジェント]]を導入した([[:en:Habash al-Hasib al-Marwazi|al-Marwazi]]説もある)。 |
|||
== 性質 == |
|||
{{main|三角関数の公式の一覧}} |
|||
一説では12世紀に[[チェスターのロバート]]が[[ラテン語]]に翻訳した際、正弦を sinus rectus と意訳し(sinusはラテン語で「湾」のこと)、現在の sine になったという。円や弦といった概念からは独立に、三角比を辺の比として角と長さの関係と捉えたのは[[16世紀]]オーストリアの[[ゲオルク・レティクス]]であるといわれる。余弦を co-sine と呼んだり、sin, cos という記号が使われるようになったりしたのは [[17世紀]]になってからであり、それが定着するのは [[18世紀]][[レオンハルト・オイラー|オイラー]]の頃である。一般角に対する三角関数を定義したのはオイラーである。 |
|||
== 三角関数の性質 == |
|||
=== 周期性 === |
=== 周期性 === |
||
[[ファイル:Circle_cos_sin.gif|thumb|300px|正円より得られる <span style="color:#00F">{{math|cos''θ''}}</span> と <span style="color:#F00">{{math|sin''θ''}}</span>]] |
|||
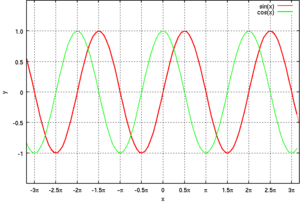
[[ファイル:Sin and cos.png|thumb|250px|sin ''x'' と cos ''x'' のグラフ。周期性が確認できる]] |
|||
[[ファイル:Sin and cos.png|thumb|300px|<span style="color:#A00">{{math|sin''x''}}</span> と <span style="color:#0A0">{{math|cos''x''}}</span> のグラフ。これらの関数の周期性が確認できる。]] |
|||
''x'' 軸の正の部分となす角は |
|||
{{mvar|x}} 軸の正の部分となす角は |
|||
:<math>t=\theta +2\pi n\ (0\le \theta <2\pi ,n\isin \mathbb{Z} )</math> |
|||
:<math>t=\theta +2\pi n\quad (0\le \theta <2\pi ,\,n\isin \mathbb{Z})</math> |
|||
と表すことができ、''θ'' を[[偏角]]、''t'' を[[一般角]]と言う。 |
|||
と表すことができ、{{mvar|θ}} を[[偏角]]、{{mvar|t}} を[[一般角]]という。 |
|||
一般角 |
一般角 {{mvar|t}} が {{math|2π}} 進めば点 {{math|P(cos''t'', sin''t'')}} は単位円上を1周し元の位置に戻る。従って、 |
||
:<math>\ |
:<math>\begin{align} |
||
\cos (t+2\pi n ) &= \cos t \\ |
|||
\sin (t+2\pi n ) &= \sin t |
|||
すなわち cos, sin は周期 2{{π}} の[[周期関数]]である。 |
|||
\end{align}</math> |
|||
すなわち三角関数 {{math|cos, sin}} は周期 {{math|2π}} の[[周期関数]]である。 |
|||
ほぼ同様に、{{math|tan, cot}} は周期 {{math|π}} の周期関数、{{math|sec, csc}} は周期 {{math|2π}} の周期関数である。 |
|||
また、{{math|cos''θ'', sin''θ''}}のグラフの形は[[正弦波]]である。 |
|||
ほぼ同様に、tan, cot は周期 {{π}} の周期関数、sec, csc は周期 2{{π}} の周期関数である。 |
|||
[[Image:Trigonometric functions.svg|right|thumb|300px|三角関数のグラフ: |
[[Image:Trigonometric functions.svg|right|thumb|300px|三角関数のグラフ: |
||
<span style="color:#00A"> |
Sine(<span style="color:#00A">青実線</span>)、 |
||
<span style="color:#0A0"> |
Cosine(<span style="color:#0A0">緑実線</span>)、 |
||
<span style="color:#A00"> |
Tangent(<span style="color:#A00">赤実線</span>)、 |
||
<span style="color:#00A"> |
Cosecant(<span style="color:#00A">青点線</span>)、 |
||
<span style="color:#0A0"> |
Secant(<span style="color:#0A0">緑点線</span>)、 |
||
<span style="color:#A00"> |
Cotangent(<span style="color:#A00">赤点線</span>)]] |
||
=== 相互関係 === |
=== 相互関係 === |
||
{{main|三角関数の公式の一覧}} |
|||
単位円上の点の座標の関数であることから、三角関数の間には多数の相互関係が存在する。 |
単位円上の点の座標の関数であることから、三角関数の間には多数の相互関係が存在する。 |
||
;基本相互関係 |
|||
==== 基本相互関係 ==== |
|||
:全て[[ピタゴラスの定理]]により証明される。 |
|||
三角関数の間に成り立つ最も基本的な恒等式の 1 つとして |
|||
:*sin{{sup|2}} ''θ'' + cos{{sup|2}} ''θ'' = 1 |
|||
: |
:<math>\sin^2 \theta + \cos^2 \theta = 1</math> |
||
が挙げられる。これは'''ピタゴラスの基本三角関数公式''' {{en|(Fundamental Pythagorean trigonometric identity)}} と呼ばれている<ref name="Leff" />。 |
|||
:*<math>\csc^2 \theta -\cot^2 \theta =\frac{1}{\sin^2 \theta} -\frac{1}{\tan^2 \theta} =1</math> |
|||
;負角・余角・補角公式 |
|||
上記の式を変形して整理すれば、以下の式が導かれる。 |
|||
:*sin(−''θ'') = −sin ''θ'' |
|||
:<math>\begin{align} |
|||
:*cos(−''θ'') = cos ''θ'' |
|||
\sec^2 \theta - \tan^2 \theta &= \frac{1}{\cos^2 \theta} - \tan^2 \theta = 1, \\ |
|||
:*tan(−''θ'') = −tan ''θ'' |
|||
\csc^2 \theta - \cot^2 \theta &= \frac{1}{\sin^2 \theta} - \frac{1}{\tan^2 \theta} = 1. |
|||
\end{align}</math> |
|||
:*<math>\cos \left( \frac{\pi}{2} -\theta \right) =\sin \theta</math> |
|||
:*<math>\tan \left( \frac{\pi}{2} -\theta \right) =\cot \theta =\frac{1}{\tan \theta}</math> |
|||
==== 負角・余角・補角公式 ==== |
|||
:*sin({{π}} − ''θ'') = sin ''θ'' |
|||
; 負角 |
|||
:*cos({{π}} − ''θ'') = −cos ''θ'' |
|||
:<math>\begin{align} |
|||
:*tan({{π}} − ''θ'') = −tan ''θ'' |
|||
\sin (-\theta ) &= -\sin\theta \\ |
|||
;{{π}}回転・{{sfrac|{{π}}|2}}回転 |
|||
\cos (-\theta ) &= \cos\theta \\ |
|||
:*sin(''θ'' + {{π}}) = −sin ''θ'' |
|||
\tan (-\theta ) &= -\tan\theta |
|||
:*cos(''θ'' + {{π}}) = −cos ''θ'' |
|||
\end{align}</math> |
|||
:*tan(''θ'' + {{π}}) = tan ''θ'' |
|||
;余角 |
|||
:*<math>\sin \left( \theta +\frac{\pi}{2} \right) =\cos \theta</math> |
|||
:<math>\begin{align} |
|||
:*<math>\cos \left( \theta +\frac{\pi}{2} \right) =-\sin \theta</math> |
|||
\sin \left( \frac{\pi}{2} - \theta \right) &= \cos \theta \\ |
|||
\cos \left( \frac{\pi}{2} - \theta \right) &= \sin \theta \\ |
|||
\tan \left( \frac{\pi}{2} - \theta \right) &= \cot \theta |
|||
\end{align}</math> |
|||
;補角 |
|||
:<math>\begin{align} |
|||
\sin (\pi - \theta ) &= \sin\theta \\ |
|||
\cos (\pi - \theta ) &= -\cos\theta \\ |
|||
\tan (\pi - \theta ) &= -\tan\theta |
|||
\end{align}</math> |
|||
=== 加法定理 === |
=== 加法定理 === |
||
:<math>\begin{align} |
|||
*sin(''α'' + ''β'') = sin ''α'' cos ''β'' + cos ''α'' sin ''β'' |
|||
\sin (x \pm y ) &= \sin x \cos y \pm \cos x \sin y \\ |
|||
\cos (x \pm y ) &= \cos x \cos y \mp \sin x \sin y \\ |
|||
\tan (x \pm y ) &= \frac{\tan x \pm \tan y}{1 \mp \tan x \tan y} |
|||
*cos(''α'' − ''β'') = cos ''α'' cos ''β'' + sin ''α'' sin ''β'' |
|||
\end{align}</math> |
|||
*<math>\tan (\alpha +\beta )=\frac{\tan \alpha +\tan \beta}{1-\tan\alpha \tan\beta}</math> |
|||
*<math>\tan (\alpha -\beta )=\frac{\tan \alpha -\tan \beta}{1+\tan \alpha \tan \beta}</math> |
|||
=== 証明 === |
|||
==== [[ピタゴラス]]の基本三角公式 ==== |
|||
1. 加法定理は、[[オイラーの公式]]から簡単に導出できる。 |
|||
三角関数および指数関数は[[冪級数]]によって[[定義]]されているものとすると、負角公式と指数法則および[[オイラーの公式]]より |
|||
:cos(''α'' + ''β'') + ''i'' sin(''α'' + ''β'') = ''e''{{sup|(''α''+''β'')''i''}}(オイラーの公式) |
|||
:<math>\begin{align}1&=e^0=e^{i\theta-i\theta}=e^{i\theta}e^{-i\theta}\\ |
|||
: = ''e{{sup|αi}}e{{sup|βi}}'' |
|||
&= \left(\cos \theta+i\sin \theta \right) \left(\cos \theta-i\sin \theta \right)\\ |
|||
: = (cos ''α'' + ''i'' sin ''α'')(cos ''β'' + ''i'' sin ''β'') |
|||
&=\sin^2 \theta+\cos^2 \theta\end{align}</math> |
|||
: = (cos ''α'' cos ''β'' − sin ''α'' sin ''β'') + ''i''(sin ''α'' cos ''β'' + cos ''α'' sin ''β'') |
|||
である。 |
|||
両辺の実部、虚部を比較すると、それぞれ sin, cos の加法公式を得る。また、 |
|||
:<math>\tan \left( \alpha \pm \beta \right) =\frac{\sin \alpha \cos \beta \pm \cos \alpha \sin \beta}{\cos \alpha \cos \beta \mp \sin \alpha \sin \beta}</math> |
|||
において分母と分子を cos ''α'' cos ''β'' で割ると tan の加法公式が得られる。 |
|||
==== 負角 ==== |
|||
この導出法は、オイラーの公式を既知とするように三角関数の導入(たとえば三角関数を[[べき級数]]として定義)していなければ証明として通用しない。 |
|||
{{math|sin}} および {{math|cos}} については、冪級数による表示から明らかである。また |
|||
:<math>\tan (-\theta ) |
|||
= \frac{\sin (-\theta )}{\cos (-\theta )} |
|||
= \frac{-\sin \theta}{\cos \theta} |
|||
= -\tan \theta</math> |
|||
である。 |
|||
==== 加法定理 ==== |
|||
2. また、単位円上の2点間の距離を求める方法でも求められる。 |
|||
[[オイラーの公式]] |
|||
[[ファイル:加法定理.png|サムネイル|右|PQ{{sup|2}} は、2通りの方法で求められる。]] |
|||
{{numBlk|:|<math>e^{iz} = \cos z + i\sin z</math>|{{equationRef|AT1-1|Euler's formula}}|RawN=.}} |
|||
単位円周上に2点 P(cos ''α'', sin ''α''), Q(cos ''β'', sin ''β'') を取り、P と Q の距離の2乗 PQ{{sup|2}} を2通りの方法で求めることを考える。(右図も参照) |
|||
と負角の公式から |
|||
:(1) 三平方の定理より求める |
|||
:<math>\cos z=\frac{e^{iz}+e^{-iz}}{2}, \sin z=\frac{e^{iz}-e^{-iz}}{2i}</math> |
|||
:PQ{{sup|2}} = (cos ''α'' − cos ''β''){{sup|2}} + (sin ''α'' − sin ''β''){{sup|2}} |
|||
を得て、指数法則 |
|||
: = 2 − 2cos ''α'' cos ''β'' − 2sin ''α'' sin''β'' |
|||
:<math>e^{z+w}=e^ze^w</math> |
|||
:(2) 余弦定理より求める |
|||
を用いれば {{math|sin, cos}} の加法定理が得られる。これらから他の三角関数についての加法定理も得られる。 |
|||
:PQ{{sup|2}} = 1{{sup|2}} + 1{{sup|2}} − 2・1・1・cos(''α'' − ''β'') |
|||
: = 2 − 2cos(''α'' − ''β'') |
|||
[[ファイル:加法定理.png|218px|サムネイル|右|{{math|PQ}}(<span style="color:#00AA00">緑</span>の線分の長さ)を求める。]] |
|||
(1), (2) より、PQ{{sup|2}} を媒介すると、 |
|||
また、[[ピタゴラスの定理]]から加法定理を示す方法が挙げられる。この方法では、円周上の任意の 2 点間の距離を 2 通りの座標系について求めることで、両者が等しいことから加法定理を導く。2 点間の距離を求めるのに三平方の定理を用いる。以下では単位円のみを取り扱うが、円の半径によらずこの方法から加法定理を得ることができる。 |
|||
:2 − 2cos ''α'' cos ''β'' − 2sin ''α'' sin ''β'' = 2 − 2cos(''α'' − ''β'') |
|||
:∴ cos(''α'' − ''β'') = cos ''α'' cos ''β'' + sin ''α'' sin ''β'' |
|||
単位円の周上に 2 点 {{math|P {{=}} (cos''p'', sin''p''), Q {{=}} (cos''q'', sin''q'')}} を取る。P と Q を結ぶ線分の長さを PQ として、その 2 乗 {{math|PQ<sup>2</sup>}} を 2 通りの方法で求めることを考える(右図も参照)。 |
|||
これより、他の3つの公式は次々に求まる。 |
|||
*''β'' に −''β'' を代入すると、 |
|||
P と Q の {{mvar|x}} 座標の差と {{mvar|y}} 座標の差から、三平方の定理を用いて {{math|PQ<sup>2</sup>}} を求める。 |
|||
:cos(''α'' + ''β'') = cos ''α'' cos ''β'' − sin ''α'' sin ''β'' |
|||
{{numBlk|:|<math>\begin{align} |
|||
*元の等式の ''α'' に <math>\frac{\pi}{2} -\alpha</math> を代入すると、 |
|||
\mathrm{PQ}^2 &= \left(\cos p - \cos q\right)^2 + \left(\sin p - \sin q\right)^2 \\ |
|||
:sin(''α'' + ''β'') = sin ''α'' cos ''β'' + cos ''α'' sin ''β'' |
|||
&= \left(\cos^2 p + \sin^2 p\right) + \left(\cos^2 q + \sin^2 q\right) - 2 \left(\cos p \cos q + \sin p \sin q\right) \\ |
|||
*この等式の ''β'' に −''β'' を代入すると、 |
|||
&= 2 - 2 \left(\cos p \cos q + \sin p \sin q\right). |
|||
:sin(''α'' − ''β'') = sin ''α'' cos ''β'' − cos ''α'' sin ''β''(導出および証明終) |
|||
\end{align}</math>|{{equationRef|PYT1|1}}}} |
|||
次に {{math|Q {{=}} (cos0, sin0) {{=}} (1, 0)}} となるような座標系を取り、同様に三平方の定理から {{math|PQ<sup>2</sup>}} を求める。この座標系に対する操作は、{{mvar|x}} 軸および {{mvar|y}} 軸を角度 {{mvar|q}} だけ回転させる操作に相当するので、{{math|P {{=}} (cos(''p'' − ''q''), sin(''p'' − ''q''))}} となる。従って、 |
|||
{{numBlk|:|<math>\begin{align} |
|||
\mathrm{PQ}^2 &= \left(\cos(p - q) - 1\right)^2 + \left(\sin(p - q) - 0\right)^2 \\ |
|||
&= 2 - 2\cos(p - q) |
|||
\end{align}</math>|{{equationRef|PYT2|2}}}} |
|||
となる。 |
|||
{{equationNote|PYT1|(1)}} と {{equationNote|PYT2|(2)}} の右辺が互いに等しいことから、次の {{math|cos}} に関する加法定理が得られる。 |
|||
{{numBlk|:|<math>\begin{align} |
|||
\cos p \cos q + \sin p \sin q= \cos(p - q). |
|||
\end{align}</math>|{{equationRef|PYT3|3}}}} |
|||
[[#相互関係|三角関数の他の性質]]を利用することで、{{equationNote|PYT3|(3)}} から {{math|sin}} の加法定理なども導くことができる。 |
|||
==== 不動点 ==== |
|||
cos の[[不動点]]は以下の式を満たし、[[ドッティ数]]とよばれる。 |
|||
:<math>\cos x = x = \cos^{-1} x \Leftrightarrow x \sim 0.739</math> |
|||
== 微積分 == |
== 微積分 == |
||
三角関数の微積分は、以下の表の |
三角関数の微積分は、以下の表のとおりである。ただし、これらの結果には様々な(一見同じには見えない)表示が存在し、この表における表示はいくつかの例であることに注意されたい。 |
||
:{|class="wikitable" |
|||
なお、以下の表の {{mvar|C}} は積分定数、{{math|ln(·)}} は[[自然対数]]である。 |
|||
|<math>f(x)</math> |
|||
:{| class="wikitable" |
|||
|<math>f'(x)</math> |
|||
!<math>f(x)</math> |
|||
![[微分]] <math>f'(x)</math> |
|||
! [[積分法|不定積分]] <math>\int f(x)\,dx</math> |
|||
|- |
|- |
||
|<math>\sin x</math> |
|<math>\sin x</math> |
||
| 163行目: | 258行目: | ||
|- |
|- |
||
|<math>\cot x</math> |
|<math>\cot x</math> |
||
|<math>-\csc^2 x=-(1+\cot^2 x)</math> |
|<math>-\csc^2 x= - \left(1+\cot^2 x \right)</math> |
||
|<math>\ln \left |\sin x\right| +C</math> |
|<math>\ln \left |\sin x\right| +C</math> |
||
|- |
|- |
||
|<math>\sec x</math> |
|<math>\sec x</math> |
||
|<math>\sec x\tan x</math> |
|<math>\sec x\tan x</math> |
||
|<math>\ln \left| \sec x+\tan x\right| +C</math> |
|<math>\ln \left| \sec x+\tan x\right| +C = \operatorname{gd}^{-1}x +C</math> |
||
|- |
|- |
||
|<math>\csc x</math> |
|<math>\csc x</math> |
||
|<math>-\csc x\cot x</math> |
|<math>-\csc x\cot x</math> |
||
|<math>-\ln \left| \csc x+\cot x\right| +C</math> |
|<math>-\ln \left| \csc x+\cot x\right| +C = \ln \left |\tan \frac{x}{2} \right| + C</math> |
||
|} |
|} |
||
ただし、{{math|gd<sup>−1</sup>''x''}} は[[グーデルマン関数]]の逆関数である。 ({{Math|1=gd<sup>-1</sup>''x'' = ln{{abs|sec ''x'' + tan ''x''}}}}) |
|||
三角関数の微分では、次の極限 |
三角関数の微分では、次の極限 |
||
:<math>\lim_{h\to 0} \frac{\sin h}{h} =1</math> |
:<math>\lim_{h\to 0} \frac{\sin h}{h} = 1</math> |
||
の成立が基本的である。このとき、sin |
の成立が基本的である。このとき、{{math|sin''x''}} の導関数が {{math|cos''x''}} であることは加法定理から従う(が、後述のようにこれは循環論法であると指摘される)。さらに余角公式 {{math|1=cos''x'' = sin ({{sfrac|π|2}} − ''x'')}} から {{math|cos''x''}} の導関数は {{math|−sin''x''}} である。すなわち、{{math|sin''x''}} は[[微分方程式]] {{math|1=''y{{'}}{{'}}''(''x'') + ''y''(''x'') = 0}} の特殊解である。また、他の三角関数の導関数も、上の事実から簡単に導ける。 |
||
=== {{math|{{Sfrac|sin''x''|''x''}}}} の {{math|''x'' → 0}} における極限 === |
|||
== 級数展開 == |
|||
{{math|{{Sfrac|sin''x''|''x''}}}} の {{math|''x'' → 0}} における極限が 1 であることを証明するときに、中心角 ''x'' ラジアンの扇形の面積を2つの三角形の面積ではさんだり<ref>{{Cite web|和書|url=http://www.geisya.or.jp/~mwm48961/kou2/d_triangle2.html|title=面積による不等式からの証明|accessdate=2015-01-20}}</ref>、弧長を線分の長さではさんだりして<ref>{{Cite web|和書|url=http://mixedmoss.com/math_reading/limit/lecture2010.pdf|title=曲線の長さによる不等式からの証明|format=PDF|accessdate=2015-01-20|page=1}}</ref><ref name="数学・物理通信">{{Cite web|和書|title=数学・物理通信|author=新関章三(元高知大学),矢野 忠(元愛媛大学)|url=http://www.phys.cs.is.nagoya-u.ac.jp/~tanimura/math-phys/mathphys-1-5.pdf|format=PDF|accessdate=2015-01-21}}</ref>、いわゆる[[はさみうちの原理]]から証明する方法がある。これは一般的な日本の高校の[[教科書]]<ref>{{Cite book|和書|author1=大矢雅則|authorlink1=大矢雅則|author2=岡部恒治 ほか13名|authorlink2=岡部恒治|title=新編 数学Ⅲ|edition=改訂版|date=2010-01-10|publisher=[[数研出版|数研出版株式会社]]|isbn=978-4-410-80166-2|oclc=676686067|ncid=BA89906770|page=53}}</ref><ref>{{Cite book|和書|author1=飯高茂|authorlink1=飯高茂|author2=松本幸夫 ほか22名|title=数学Ⅲ|date=2008-02-10|publisher=[[東京書籍|東京書籍株式会社]]|isbn=4-487-15513-4|oclc=76931848|ncid=BA71854010|page=49}}ほか</ref>にも載っているものであるが、[[循環論法]]であるため論理が破綻しているという主張がなされることがある<ref name="A">{{Cite web|和書|url=http://sci-tech.ksc.kwansei.ac.jp/~kawanaka/sinx.pdf|title=循環論法で証明になっていない|accessdate=2015-01-18|author=川中宣明|format=PDF|page=1}}</ref>{{Sfn|杉浦光夫|1980|p=175}}。ここで問題となるのは、証明に面積やラジアン、弧長が利用されていることである。例えば面積について言えば、面積は積分によって定義されるものであるとすると、扇形の面積を求めるには三角関数の積分が必要となる。三角関数の積分をするには三角関数の微分ができなければならないが、三角関数を微分するにはもとの極限が必要になる。このことが循環論法と呼ばれているのである。 |
|||
三角関数は以下のように[[テイラー級数]]に展開される。[[解析学]]では、幾何的な性質へ言及せず、これらの表示を三角関数の[[定義]]とすることがある。''z'' は任意の複素数、''B{{sub|n}}'' は[[ベルヌーイ数]]、''E{{sub|n}}'' は [[オイラー数]]である。 |
|||
{{Indent|<math>\sin z=\sum^{\infin}_{n=0} \frac{(-1)^n}{(2n+1)!} z^{2n+1}\quad\mbox{ for all } z</math><br> |
|||
単位円板の面積が {{π}} であることを自明な概念と考えてしまえば循環論法にはならないが、これはいくつかの決められた公理・定義から論理的演繹のみによって証明されたものだけを正しいと考える現代数学の思想とは相反するものである。循環論法を回避する方法の 1 つは、正弦関数と余弦関数を上述のような無限級数で定義するものである(これは三角関数の標準的な定義の 1 つである。また、この無限級数の収束半径は無限大である(すなわち任意の実数や複素数で収束する))。この定義に基づいて |
|||
<math>\cos z=\sum^{\infin}_{n=0} \frac{(-1)^n}{(2n)!} z^{2n}\quad\mbox{ for all } z</math> |
|||
<math>\ |
:<math>\lim_{x \to 0}\frac{\sin\,x}{x}=1</math> |
||
を示すことができる。 |
|||
<math>\csc z=\sum^{\infin}_{n=0} \frac{(-1)^n (2-2^{2n}) B_{2n}}{(2n)!} z^{2n-1} \quad \mbox{ for } 0<|z|<\pi</math> |
|||
しかしながら、このように定義された三角関数が、本来持つべき幾何学的な性質を有しているかどうかは全く明らかなことではない。これを確かめるためには、三角関数の諸公式(周期性やピタゴラスの基本三角関数公式等)を証明し、また円周率は、余弦関数の正の最小の零点(つまり、{{math|cos''x'' {{=}} 0}} となる正の最小の値)の存在を示し、その 2 倍と定義する。すると、<math>x\mapsto(\cos x, \sin x)</math> が区間 {{math|[0, 2{{π}})}} から単位円周への(「反時計まわりの」)[[全単射]]であることを示すことができる。(連続微分可能な)曲線の長さを積分によって定義すれば、単位円周の長さが {{math|2{{π}}}} であることなどがわかり、上のように定義された三角関数や円周率は、初等幾何での三角関数や円周率の素朴な定義と同じものであることが分かった <ref group="注釈">三角関数、円周率、曲線の長さ等の定義の仕方は、複数の流儀がある。</ref>{{sfn|杉浦光夫|1980|pp=175-185}}。 |
|||
<math>\sec z=\sum^{\infin}_{n=0} \frac{(-1)^n E_{2n}}{(2n)!} z^{2n} \quad \mbox{ for } |z|<\frac{\pi}{2}</math> |
|||
<math>\cot z=\sum^{\infin}_{n=0} \frac{(-1)^n 2^{2n} B_{2n}}{(2n)!} z^{2n-1} \quad \mbox{ for } 0<|z|<\pi</math> |
|||
}} |
|||
== 無限乗積展開 == |
== 無限乗積展開 == |
||
三角関数 |
{{main|三角関数の無限乗積展開}} |
||
三角関数は以下のように無限乗積として書ける。 |
|||
:<math>\sin \pi z=\pi z\prod_{n=1}^{\infty}{\left(1-\frac{z^2}{n^2}\right)}</math> |
|||
:<math>\begin{align} |
|||
<math>\cos \pi z=\prod_{n=1}^\infty \left\{ 1-\frac{z^2}{(n-\frac{1}{2})^2}\right\}</math> |
|||
\sin \pi z &= \pi z \prod_{n=1}^{\infty}{\left(1-\frac{z^2}{n^2} \right)} \\ |
|||
\cos \pi z &= \prod_{n=1}^\infty \left\{ 1-\frac{z^2}{(n - \frac{1}{2})^2} \right\} |
|||
\end{align}</math> |
|||
== 部分分数展開 == |
== 部分分数展開 == |
||
三角関数 |
{{main|三角関数の部分分数展開}} |
||
三角関数は以下のように部分分数に展開される。 |
|||
{{Indent| |
|||
:<math>\begin{align} |
|||
<math>\pi \cot \pi z=\lim_{N\to\infty} \sum_{n=-N}^N \frac{1}{z+n} =\frac{1}{z} +\sum_{n=1}^\infty \frac{2z}{z^2 -n^2}</math><br> |
|||
\pi \cot \pi z &= \lim_{N \to \infty} \sum_{n = -N}^N \frac{1}{z + n} |
|||
= \frac{1}{z} + \sum_{n = 1}^\infty \frac{2z}{z^2 -n^2} \\ |
|||
\pi \tan \pi z &= - \lim_{N \to \infty} \sum_{n = -N}^N \frac{1}{z + 1/2 + n} |
|||
= -\sum_{n = 0}^\infty \frac{2z}{z^2 - (n + 1/2 )^2} \\ |
|||
}} |
|||
\frac{\pi}{\sin \pi z} &= \lim_{N \to \infty} \sum_{n = -N}^N \frac{(-1)^n}{z + n} |
|||
= \frac{1}{z} + \sum_{n = 1}^\infty \frac{(-1)^n 2z}{z^2 - n^2} \\ |
|||
\frac{\pi}{\cos \pi z} &= \lim_{N \to \infty} \sum_{n = -N}^N \frac{(-1)^n}{z + 1/2 +n} |
|||
= -\sum_{n = 0}^\infty \frac{(-1)^n (2n + 1)}{z^2 - (n + 1/2 )^2} |
|||
\end{align}</math> |
|||
== 逆三角関数 == |
== 逆三角関数 == |
||
{{main|逆三角関数}} |
|||
三角関数の定義域を適当に制限したものの[[逆関数]]を'''逆三角関数'''(ぎゃくさんかくかんすう、<em lang="en">inverse trigonometric function</em>)と呼ぶ。逆三角関数は逆関数の記法に則り、元の関数の記号に −1 を右肩に付して表す。たとえば'''逆'''正弦関数(ぎゃくせいげんかんすう、<span lang="en">inverse sine</span>; インバース・サイン)は sin{{sup|−1}} ''x'' などと表す。arcsin, arccos などの記法もよく用いられる。 |
|||
三角関数の定義域を適当に制限したものの逆関数を'''逆三角関数'''(ぎゃくさんかくかんすう、{{lang-en-short|''inverse trigonometric function''}})と呼ぶ。逆三角関数は逆関数の記法に則り、元の関数の記号に {{math|−1}} を右肩に付して表す。たとえば'''逆'''正弦関数(ぎゃくせいげんかんすう、{{lang-en-short|inverse sine;}} インバース・サイン)は {{math|sin<sup>−1</sup>''x''}} などと表す。{{math|arcsin, arccos, arctan}} などの記法もよく用いられる。数値計算などにおいては、これらの逆関数はさらに {{math|asin, acos, atan}} などと書き表される。 |
|||
:<math>x=\sin y \iff y=\sin^{-1} x</math> |
|||
:<math> |
:<math>\begin{align} |
||
x = \sin y &\iff y = \sin^{-1} x \\ |
|||
x = \cos y &\iff y = \cos^{-1} x \\ |
|||
x = \tan y &\iff y = \tan^{-1} x \\ |
|||
x = \cot y &\iff y = \cot^{-1} x \\ |
|||
x = \sec y &\iff y = \sec^{-1} x \\ |
|||
である。逆関数は逆数ではないので注意したい。逆数との混乱を避けるために、逆正弦関数 sin{{sup|−1}} ''x'' を arcsin ''x'' と書く流儀もある。一般に周期関数の逆関数は[[関数 (数学)#多変数関数と多価関数|多価関数]]になるので、通常は逆三角関数を一価[[連続]]なる[[枝]]に制限して考えることが多い。たとえば、便宜的に'''[[主値]]'''と呼ばれる枝を |
|||
x = \csc y &\iff y = \csc^{-1} x |
|||
:<math>-\frac{\pi}{2} \le \sin^{-1} x\le \frac{\pi}{2}</math> |
|||
\end{align}</math> |
|||
である。逆関数は'''[[逆数]]ではない'''ので注意したい。逆数との混乱を避けるために、逆正弦関数 '''{{math|sin<sup>−1</sup>''x''}}''' を '''{{math|arcsin''x''}}''' と書く流儀もある。一般に周期関数の逆関数は[[関数 (数学)#多変数関数と多価関数|多価関数]]になるので、通常は逆三角関数を一価[[連続 (数学)|連続]]なる枝に制限して考えることが多い。たとえば、便宜的に'''[[主値]]'''と呼ばれる枝を |
|||
:<math>-\frac{\pi}{2} <\tan^{-1} x<\frac{\pi}{2}</math> |
|||
:<math>\begin{align} |
|||
のように選ぶことが多い。またこのとき、制限があることを強調するために、Sin{{sup|−1}} ''x'', Arcsin ''x'' のように頭文字を大文字にした表記がよく用いられる。 |
|||
-\frac{\pi}{2} &\le \sin^{-1} x \le \frac{\pi}{2} \\ |
|||
0 &\le \cos^{-1} x \le \pi \\ |
|||
-\frac{\pi}{2} &< \tan^{-1} x < \frac{\pi}{2} |
|||
\end{align}</math> |
|||
のように選ぶことが多い。またこのとき、制限があることを強調するために、'''{{math|Sin<sup>−1</sup>''x'', Arcsin ''x''}}''' のように頭文字を大文字にした表記がよく用いられる。 |
|||
== 複素関数 |
== 複素関数として == |
||
{{math|exp ''z'', cos ''z'', sin ''z''}} の[[#級数によるもの|級数による定義]]から、[[オイラーの公式]] {{math|exp (''iz'') {{=}} cos ''z'' + ''i'' sin ''z''}} を導くことができる。この公式から下記の 2 つの等式 |
|||
:<math>\begin{align} |
|||
{{Indent|exp ''ix'' <nowiki>=</nowiki> cos ''x'' + ''i'' sin ''x''<br> |
|||
exp( |
\exp(iz) &= e^{iz} = \cos z + i \sin z,\\ |
||
\exp(-iz) &= e^{-iz} = \cos z - i \sin z |
|||
}} |
|||
\end{align}</math> |
|||
が得られるから、これを連立させて解くことにより、正弦関数・余弦関数の[[初等関数]]としての表現が可能となる。即ち、 |
|||
が得られるから、これを連立させて解くことにより、正弦関数・余弦関数の[[指数関数]]を用いた表現が可能となる。すなわち、 |
|||
:<math>\cos x=\frac{e^{ix} +e^{-ix}}{2},</math> |
|||
:<math>\ |
:<math>\begin{align} |
||
\cos z &= \frac{e^{iz} + e^{-iz}}{2} ,\\ |
|||
この事実を用いて、三角関数の定義域を複素数全体に拡張することができる。まず、 |
|||
\sin z &= \frac{e^{iz} - e^{-iz}}{2i} |
|||
\end{align}</math> |
|||
<math>\sin ix=\frac{e^{-x} -e^x}{2i} = i\sinh x</math>}} |
|||
が成り立つ。この事実により、級数によらずこの等式をもって[[複素数]]の正弦・余弦関数の定義とすることもある。また、 |
|||
である。ここで cosh ''x'', sinh ''x'' は[[双曲線関数]]を指す。この等式は三角関数と双曲線関数の関係式と捉えることもできる。任意の複素数 ''z'' は ''z'' = ''x'' + ''iy'' (''x'', ''y'' ∈ '''R''') と表現できるから、加法定理より |
|||
:<math>\begin{align} |
|||
:cos ''z'' = cos(''x'' + ''iy'') = cos ''x'' cosh ''y'' − ''i'' sin ''x'' sinh ''y'',<br> |
|||
\cos(iz) &= \frac{e^{-z} +e^z}{2} = \cosh z, \\ |
|||
:sin ''z'' = sin(''x'' + ''iy'') = sin ''x'' cosh ''y'' + ''i'' cos ''x'' sinh ''y'' |
|||
\sin(iz) &= \frac{e^{-z} -e^z}{2i} = i\sinh z |
|||
が成り立つ。これこそが正弦関数・余弦関数の定義域を複素数全体に拡張したものである。他の三角関数も正弦関数と余弦関数の四則演算によって定義できるから、結局全ての三角関数は定義域を複素数全体に拡張できることが分かる。 |
|||
\end{align}</math> |
|||
<gallery> |
|||
が成り立つ。ここで {{math|cosh ''z'', sinh ''z''}} は[[双曲線関数]]を表す。この等式は三角関数と双曲線関数の関係式と捉えることもできる。[[複素数]] {{mvar|z}} を {{math|''z'' {{=}} ''x'' + ''iy'' (''x'', ''y'' ∈ '''R''')}} と表現すると、加法定理より |
|||
ファイル:Cos Re.png|cos(''x'' + ''iy'') の実部のグラフ |
|||
:<math>\begin{align} |
|||
ファイル:Cos Im.png|cos(''x'' + ''iy'') の虚部のグラフ |
|||
\cos z &= \cos(x + iy) = \cos x \cosh y - i \sin x \sinh y, \\ |
|||
ファイル:Sin Re.png|sin(''x'' + ''iy'') の実部のグラフ |
|||
\sin z &= \sin(x + iy) = \sin x \cosh y + i \cos x \sinh y |
|||
ファイル:Sin Im.png|sin(''x'' + ''iy'') の虚部のグラフ |
|||
\end{align}</math> |
|||
が成り立つ。 |
|||
他の三角関数は {{math|csc''z'' {{=}} 1 / sin''z''}}, {{math|sec''z'' {{=}} 1 / cos''z''}}, {{math|tan''z'' {{=}} sin''z'' / cos''z''}}, {{math|cot''z'' {{=}} cos''z'' / sin''z''}} によって定義できる。 |
|||
<gallery perrow="2" widths="249px" heights="146px"> |
|||
ファイル:Cos Re.png|{{math|cos(''x'' + ''iy'')}} の実部のグラフ |
|||
ファイル:Cos Im.png|{{math|cos(''x'' + ''iy'')}} の虚部のグラフ |
|||
ファイル:Sin Re.png|{{math|sin(''x'' + ''iy'')}} の実部のグラフ |
|||
ファイル:Sin Im.png|{{math|sin(''x'' + ''iy'')}} の虚部のグラフ |
|||
</gallery> |
</gallery> |
||
== 球面三角法 == |
== 球面三角法 == |
||
{{main|球面三角法}} |
{{main|球面三角法}} |
||
球面の三角形ABC の内角を ''a'', ''b'', ''c'', 各頂点の対辺に関する球の中心角を ''α'', ''β'', ''γ'' とするとき、次のような関係が成立する。余弦公式や正弦余弦公式は式の対称性により各記号を入れ替えたものも成立する。 |
球面の三角形 ABC の内角を {{math|''a'', ''b'', ''c''}}, 各頂点の対辺に関する球の中心角を {{math|''α'', ''β'', ''γ''}} とするとき、次のような関係が成立する。余弦公式や正弦余弦公式は式の対称性により各記号を入れ替えたものも成立する。 |
||
; 正弦公式 |
|||
: {{math|sin''a'' : sin''b'' : sin''c'' {{=}} sin''α'' : sin''β'' : sin''γ''}} |
|||
; 余弦公式 |
|||
: {{math|cos''a'' {{=}} −cos''b'' cos''c'' + sin''b'' sin''c'' cos''α''}} |
|||
; 余弦公式 |
|||
: {{math|cos''α'' {{=}} cos''β'' cos''γ'' + sin''β'' sinγ cos''a''}} |
|||
; 正弦余弦公式 |
|||
: {{math|sin''a'' cos''β'' {{=}} cos''b'' sin''c'' − sin''b'' cos''c'' cos''α''}} |
|||
== 語源 == |
|||
三角関数の英語の名称の語源について記す。 |
|||
sineはもとはchord-half(半弦)を意味する[[サンスクリット]] jya ̄-ardha起源であり、省略形ji ̄va ̄が[[アラビア語]]に音訳されてjibaとなったが、1145年に[[チェスターのロバート]]が[[フワーリズミー]]の{{仮リンク|ヒサーブ・アル=ジャブル・ワル=ムカーバラ|en| The Compendious Book on Calculation by Completion and Balancing}}を[[ラテン語]]に翻訳する際に、jaibと混同した事で胸、湾の意味のsinusと翻訳された<ref>Victor J. Katz (2008), ''A History of Mathematics'', Boston: Addison-Wesley, 3rd. ed., p. 253, sidebar 8.1. {{cite web |url=http://deti-bilingual.com/wp-content/uploads/2014/06/3rd-Edition-Victor-J.-Katz-A-History-of-Mathematics-Pearson-2008.pdf |title=Archived copy |accessdate=2020-12-22 |url-status=live |archiveurl=https://web.archive.org/web/20150414065531/http://deti-bilingual.com/wp-content/uploads/2014/06/3rd-Edition-Victor-J.-Katz-A-History-of-Mathematics-Pearson-2008.pdf |archivedate=2015-04-14 }}</ref><ref>{{cite web|title=The Etymology of “Sine”|url= http://www-math.ucdenver.edu/~wcherowi/courses/history2/hmsine.html|website= Bill Cherowitzo's Home Page, Mathematical Department, University of Colorado at Denver|accessdate=December 22, 2020}}</ref>。 |
|||
tangentは”touching”を意味するラテン語tangens由来で、secantは”cutting”を意味するラテン語secans由来である<ref>New Oxford American Dictionary</ref>。 |
|||
cosine、cotangent、cosecantはそれぞれ[[接頭辞]]のco-がついた形であり、co-は{{仮リンク|cofunction|en|cofunction}}と共通し、これは{{仮リンク|compliment angle|en|complementary angle}}([[直角三角形]]の[[直角]]でないもう一つの角、余角)に対するsine、tangent、secantという意味である。cosine、cotangentが初めて書かれた形で確認されるのは1620年の[[エドマンド・ガンター]]による”Canon triangulorum”の中である。ラテン語のcosinusとして登場し、これはsinus complementiの略である<ref>{{Cite journal |author=Roegel, Deni |year=2010 |title=A reconstruction of Gunter's Canon triangulorum (1620) |url=https://inria.hal.science/inria-00543938/document}}</ref>。 |
|||
日本語の正弦、余弦に関しては、[[徐光啓]]らが編纂した『崇禎暦書』の中で、{{仮リンク|羅雅谷|en|Giacomo Rho}}が1631年に著した『測量全義』の八線のうちに見られる<ref>{{Cite journal|和書|author=杜石然 |date=2001-07 |url=https://archives.bukkyo-u.ac.jp/repository/baker/rid_CB000100001982 |title=イエズス会士と西洋数学の伝入 |journal=中国言語文化研究 |ISSN=1346-6305 |publisher=佛教大学中国言語文化研究会 |volume=1 |pages=1-22 |naid=110007974156 |CRID=1050287838661758848 |ref=harv}}</ref><ref name="sitekikousatsu" >{{Cite journal|和書|author=伊達文治 |date=2015-03 |url=https://hdl.handle.net/10513/00006983 |title=三角法と対数の教材に関する史的考察 |journal=上越教育大学数学研究 |publisher=上越教育大学数学教室 |volume=30 |pages=13-22 |hdl=10513/00006983 |naid=120005703229 |CRID=1050845763704678656}}</ref>。「正」の漢字には、「真向かいの」「主となるもの」という意味がある<ref>角川新字源 改訂版 角川学芸出版</ref>。 |
|||
{{see also|[[三角法#歴史|三角法の歴史]]}} |
|||
== 脚注 == |
|||
{{脚注ヘルプ}} |
|||
=== 注釈 === |
|||
{{Notelist}} |
|||
=== 出典 === |
|||
{{Reflist|2|refs= |
|||
<ref name="三角関数と円周率" >{{Cite web|和書|title=三角関数と円周率|author=幡谷泰史|coauthors=廣澤史彦<!--|first1=泰史|last1=幡谷|first2=史彦|last2=廣澤-->|url=https://ds0n.cc.yamaguchi-u.ac.jp/~hirosawa/other/menkyo/text.pdf|format=PDF|accessdate=2023-09-20}}</ref> |
|||
<ref name="三角関数のさまざまな定義" >{{Cite web|和書|title=三角関数のさまざまな定義|first=等|last=瓜生|url=http://staff.miyakyo-u.ac.jp/~h-uri/blog/archive/lecture/sugakuenshu/2000/sankaku.pdf|format=PDF|accessdate=2014-10-08}}{{404|date=2023-09}}</ref> |
|||
<ref name="三角関数の研究">{{Cite journal|和書|author=山口格 |title=三角関数の研究 |journal=教授学の探究 |issn=0288-3511 |publisher=北海道大学教育学部教育方法学研究室 |year=1989 |month=mar |issue=7 |pages=1-23 |naid=120000962860 |url=https://hdl.handle.net/2115/13556}}</ref> |
|||
<ref name="NaitoFourierLecture1999">{{Cite web|和書|first=久資|last=内藤|url=https://www.math.nagoya-u.ac.jp/~naito/lecture/1999/Fourier/note.pdf|format=PDF|title=1999年度後期「Fourier 変換とその応用 "403 Forbidden"|year=1999|accessdate=2014-10-17}}{{404|date=2023-09}}</ref> |
|||
<ref name="Leff">{{Cite book|title=PreCalculus the Easy Way|first=Lawrence S.|last=Leff|url=https://books.google.co.jp/books?id=y_7yrqrHTb4C&pg=PA296&redir_esc=y&hl=ja|isbn=0-7641-2892-2|page=296|edition=7th|publisher=Barron's Educational Series|year=2005|ref=harv}}</ref> |
|||
<!-- |
|||
<ref name="指数函数の定義と基本的性質">{{cite web|url=http://www.math.sci.hokudai.ac.jp/~ozawa/pdf/sisu.pdf|format=PDF|title=指数函数の定義と基本的性質|accessdate=2015-3-27}}{{リンク切れ|date=2021年6月}}</ref> |
|||
--> |
|||
}} |
|||
== 参考文献 == |
|||
* {{cite book||first=Eli|last=Maor|authorlink=:en:Eli Maor|title=Trigonometric Delights|year=1998|publisher=[[プリンストン大学|Princeton University Press]]|isbn=978069105754-5|ref=harv}} |
|||
* {{cite book|和書|author=志賀浩二|authorlink=志賀浩二|title=数の大航海―対数の誕生と広がり|date=1999-07|publisher=[[日本評論社]]|isbn=978-4-535-78289-1|ref=harv}} |
|||
* {{cite book|和書|author=高瀬正仁|authorlink=高瀬正仁|title=古典的難問に学ぶ微分積分|date=2013-07|publisher=[[共立出版]]|isbn=978-4-320-11041-0|ref=harv}} |
|||
* {{cite book||first=Ivan Matveyevich|last=Vinogradov|authorlink=:en:Ivan Matveyevich Vinogradov|title=The Method of Trigonometrical Sums in the Theory of Numbers|edition=revised|date=2004-09-10|publisher=Dover|isbn=978-048643878-8|ref=harv}} |
|||
* {{cite book|和書|author1=黒川信重|authorlink1=黒川信重|author2=小山信也|authorlink2=小山信也|title=多重三角関数論講義|date=2010-11-08|publisher=[[日本評論社]]|isbn=978-4-535-785557| |
|||
ref=harv}} ※ 通常の三角関数、ガンマ関数、ゼータ関数などを「多重化」した特殊関数の理論の構築。 |
|||
* 黒川信重:「現代三角函数論」、岩波書店、ISBN 978-4-00-005327-3 (2013年11月7日). ※ 通常の三角関数、ガンマ関数、ゼータ関数などを「多重化」した特殊関数の理論の構築。 |
|||
* {{Cite book|和書|author=杉浦光夫|authorlink=杉浦光夫|title=解析入門I|year=1980|publisher=[[東京大学出版会]]|isbn=978-4-13-062005-5|series=基礎数学2|ref=harv}} |
|||
* {{Cite book|和書|author=黒田成俊|authorlink=黒田成俊|title= 微分積分|year=2002|publisher=共立出版|isbn=978-4320015531|series=共立講座21世紀の数学 第1巻|ref=harv}} |
|||
* {{Cite book|和書|author=高木貞治|authorlink=高木貞治|title=定本 解析概論|year=2010|publisher=岩波書店|isbn=978-4000052092|edition=改訂第3版|ref=harv}} |
|||
* {{Cite book|和書|author=小平邦彦|authorlink=小平邦彦|title=解析入門I|year=2003|publisher=岩波書店|isbn=978-4000051927|edition=軽装版|ref=harv}} |
|||
== 関連項目 == |
== 関連項目 == |
||
*[[正弦定理]] |
* [[正弦定理]] |
||
*[[余弦定理]] |
* [[余弦定理]] |
||
*[[正接定理]] |
* [[正接定理]] |
||
*[[球面三角法]] |
* [[球面三角法]] |
||
*[[コサイン4乗則]] |
* [[コサイン4乗則]] |
||
* [[ベクトルのなす角]] - cos 関数を用いて表現される。 |
|||
* [[ドット積]] |
|||
* [[クロス積]] |
|||
* [[ベッセル関数]] |
|||
* [[sinc関数]] |
|||
* [[指数関数]] |
|||
* [[双曲線関数]] |
|||
* [[オイラーの公式]] |
|||
* [[円_(数学)|円]] - 正円の三角関数との関係 |
|||
* [[ベジェ曲線]] - 三角関数のベジエ曲線による近似 |
|||
* [[テイラー展開]] - [[コンピュータ]]上での三角関数の実装に使用 |
|||
* [[算数チャチャチャ]] - 歌詞に三角関数の問題の解き方が含まれる |
|||
*[[3次元コンピュータグラフィックス]] |
|||
== 外部リンク == |
== 外部リンク == |
||
{{ウィキプロジェクトリンク|数学|[[画像:Nuvola apps edu mathematics blue-p.svg|34px|Project:数学]]}} |
|||
*{{MathWorld|urlname=TrigonometricFunctions|title=Trigonometric Functions}} |
|||
{{ウィキポータルリンク|数学|[[画像:Nuvola apps edu mathematics-p.svg|34px|Portal:数学]]}} |
|||
*[http://www.csuchico.edu/~jhudson/pdf/trigtabl.pdf 三角比の近似値表] |
|||
* [http://www.csuchico.edu/~jhudson/pdf/trigtabl.pdf 三角比の近似値表] |
|||
* {{MathWorld|urlname=TrigonometricFunctions|title=Trigonometric Functions}} |
|||
*[http://core.kyoto3.jp/trigo.html 江戸時代の三角関数表](これなあに) |
|||
* {{Kotobank}} |
|||
{{Normdaten}} |
|||
{{DEFAULTSORT:さんかくかんすう}} |
{{DEFAULTSORT:さんかくかんすう}} |
||
[[Category:解析学]] |
[[Category:解析学]] |
||
[[Category:三角法]] |
[[Category:三角法]] |
||
[[Category:三角関数|*]] |
|||
[[Category:初等関数]] |
[[Category:初等関数]] |
||
[[Category:数学に関する記事]] |
[[Category:数学に関する記事]] |
||
{{Link FA|ca}} |
|||
{{Link GA|pl}} |
|||
{{Link FA|km}} |
|||
{{Link GA|zh}} |
|||
2025年1月4日 (土) 15:50時点における最新版
三角関数(さんかくかんすう、英: trigonometric function)とは、平面三角法における、角度の大きさと線分の長さの関係を記述する関数の族、およびそれらを拡張して得られる関数の総称である。鋭角を扱う場合、三角関数の値は対応する直角三角形の二辺の長さの比(三角比)である。三角法に由来する三角関数という呼び名のほかに、単位円を用いた定義に由来する円関数(えんかんすう、circular function)という呼び名がある。
三角関数には以下の6つがある。なお、正弦、余弦、正接の3つのみを指して三角関数と呼ぶ場合もある。
- 正弦(せいげん)、sin(sine)
- 余弦(よげん)、cos(cosine)
- 正接(せいせつ)、tan(tangent)
- 正割(せいかつ)、sec(secant)
- 余割(よかつ)、csc,cosec(cosecant)
- 余接(よせつ)、cot(cotangent)
特に sin, cos は幾何学的にも解析学的にも良い性質をもっているので、様々な分野で用いられる。例えば、波や信号などは正弦関数と余弦関数とを組み合わせて表現することができる。この事実はフーリエ級数およびフーリエ変換の理論として知られ、音声などの信号の合成や解析の手段として利用されている。ベクトルのクロス積や内積は正弦関数および余弦関数を用いて表すことができ、ベクトルを図形に対応づけることができる。初等的には、三角関数は実数を変数とする1変数関数として定義される。三角関数の変数に対応するものとしては、図形のなす角度や、物体の回転角、波や信号のような周期的なものにおける位相などが挙げられる。
三角関数に用いられる独特な記法として、三角関数の冪乗と逆関数に関するものがある。通常、関数 f(x) の累乗は (f(x))2 = f(x)・f(x) や (f(x))−1 = 1/f(x) のように書くが、三角関数の累乗は sin2x のように書かれることが多い。逆三角関数については通常の記法 (f−1(x)) と同じく、sin−1x などと表す(この文脈では、三角関数の逆数は分数を用いて 1/sin x または (sin x)−1 のように表される)。文献または著者によっては、通常の記法と三角関数に対する特殊な記法との混同を避けるため、三角関数の累乗を通常の関数と同様にすることがある。また、三角関数の逆関数として −1 を添え字にする代わりに関数の頭に arc を付けることがある(たとえば sin の逆関数として sin−1 の代わりに arcsin を用いる。Arc を付けて Arcsin と表すこともある)。
三角関数に似た性質をもつ関数として、指数関数、双曲線関数、ベッセル関数などがある。また、三角関数を利用して定義される関数としてしばしば応用されるものにsinc関数がある。
定義
[編集]直角三角形によるもの
[編集]
斜辺AB = h (hypotenuse)
対辺BC = a (opposite side)
底辺AC = b (adjacent side、隣辺)
直角三角形において、1 つの鋭角の大きさが決まれば、三角形の内角の和は 180°であることから他の 1 つの鋭角の大きさも決まり、3 辺の比も決まる。ゆえに、角度に対して辺比(三角比)の値を与える関数を考えることができる。
∠C を直角とする直角三角形 ABC において、斜辺AB、∠A の対辺BC、底辺(隣辺)CA の辺の長さをそれぞれ AB = h, BC = a, CA = b と表す(図を参照)。∠A = θ に対して三角形の辺の比 h : a : b が決まることから、
という 6 つの値が定まる。それぞれ正弦:sin(sine; サイン)、余弦:cos(cosine; コサイン)、正接:tan(tangent; タンジェント)、正割:sec(secant; セカント)、余割:cosec(cosecant; コセカント)、余接:cot(cotangent; コタンジェント)と呼び、まとめて三角比と呼ばれる。ただし cosec は長いので csc と略記することも多い。
| _弦 | _接 | _割 | ∠C を直角とする直角三角形 ABC h = 斜辺AB a = 対辺BC b = 底辺AC | ||||
|---|---|---|---|---|---|---|---|
| 正_ | 正弦 (sin) |
正接 (tan) |
正割 (sec) |
||||
| 余_ | 余弦 (cos) |
余接 (cot) |
余割 (csc) |
||||
ある正角 ∠A に対する余弦、余割、余接はその角 ∠A の余角 (co-angle)に対する正弦、正割、正接として定義される。ここで余角とは「鋭角(正角)に対し合わせて直角となる角」を指し、この場合は 正角∠Aに対する余角は∠Bとなる。
三角比は平面三角法に用いられ、巨大な物の大きさや遠方までの距離を計算する際の便利な道具となる。角度 θ の単位は、通常度またはラジアンである。
三角比、すなわち三角関数の直角三角形を用いた定義は、直角三角形の鋭角に対して定義されるため、その定義域は θ が 0° から 90° まで(0 から π / 2 まで)の範囲に限られる。また、θ = 90° (= π / 2) の場合 sec, tan が、θ = 0°(= 0) の場合 csc, cot がそれぞれ定義されない。これは分母となる辺の比の大きさが 0 になるためゼロ除算が発生し、その除算自体が数学的に定義されないからである。一般の角度に対する三角関数を得るためには、三角関数について成り立つ何らかの定理を指針として、定義の拡張を行う必要がある。単位円による定義は初等幾何学におけるそのような拡張の例である。他に同等な方法として、正弦定理や余弦定理を用いる方法などがある。
単位円によるもの
[編集]
2 次元ユークリッド空間 R2 における単位円 {x(t)}2 + {y(t)}2 = 1 上の点を A = (x(t), y(t)) とする。反時計回りを正の向きとして、原点と円周を結ぶ線分 OA と x 軸のなす角の大きさ ∠xOA を媒介変数 t として選ぶ。このとき実数の変数 t に対する三角関数は以下のように定義される。
これらは順に正弦関数 (sine function)、余弦関数 (cosine function)、正接関数(tangent function) と呼ばれる。さらにこれらの逆数として以下の 3 つの関数が定義される。
これらは順に余割関数 (cosecant function)、正割関数 (secant function)、余接関数 (cotangent function) と呼ばれ、sin, cos, tan と合わせて三角関数と総称される。特に csc, sec, cot は割三角関数(かつさんかくかんすう)と呼ばれることがある。
この定義は 0 < t < π / 2 の範囲では直角三角形による定義と一致する。
級数によるもの
[編集]角度、辺の長さといった幾何学的な概念への依存を避けるため、また定義域を複素数に拡張するために、級数(他の定義を採用した三角関数のテイラー展開に一致する)を用いて定義することもできる。この定義は実数の範囲では単位円による定義と一致する。以下の級数は共に示される収束円内で収束する。
微分方程式によるもの
[編集]実関数 f(x) の二階線型常微分方程式の初期値問題
の解として cosx を定義し、sinx を −d (cosx)/dx として定義できる[1][2]。上記の式を 1 階の連立常微分方程式に書き換えると、g(x) = f '(x) として、
および初期条件 f(0) = 1, g(0) = 0 となる。
他の定義
[編集]この他にも定積分による(逆三角関数を用いた)定義や複素平面の角の回転による定義などが知られている[1][3][4][5][6][7]。
性質
[編集]周期性
[編集]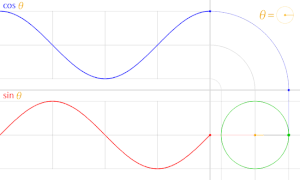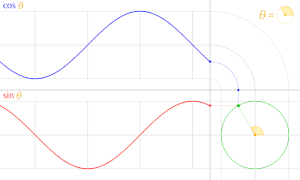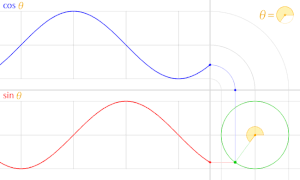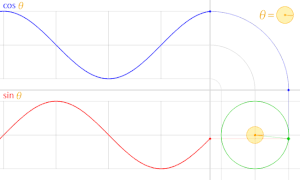
x 軸の正の部分となす角は
一般角 t が 2π 進めば点 P(cost, sint) は単位円上を1周し元の位置に戻る。従って、
すなわち三角関数 cos, sin は周期 2π の周期関数である。
ほぼ同様に、tan, cot は周期 π の周期関数、sec, csc は周期 2π の周期関数である。
また、cosθ, sinθのグラフの形は正弦波である。

相互関係
[編集]単位円上の点の座標の関数であることから、三角関数の間には多数の相互関係が存在する。
基本相互関係
[編集]三角関数の間に成り立つ最も基本的な恒等式の 1 つとして
が挙げられる。これはピタゴラスの基本三角関数公式 (Fundamental Pythagorean trigonometric identity) と呼ばれている[8]。
上記の式を変形して整理すれば、以下の式が導かれる。
負角・余角・補角公式
[編集]- 負角
- 余角
- 補角
加法定理
[編集]証明
[編集]三角関数および指数関数は冪級数によって定義されているものとすると、負角公式と指数法則およびオイラーの公式より
である。
負角
[編集]sin および cos については、冪級数による表示から明らかである。また
である。
加法定理
[編集]と負角の公式から
を得て、指数法則
を用いれば sin, cos の加法定理が得られる。これらから他の三角関数についての加法定理も得られる。

また、ピタゴラスの定理から加法定理を示す方法が挙げられる。この方法では、円周上の任意の 2 点間の距離を 2 通りの座標系について求めることで、両者が等しいことから加法定理を導く。2 点間の距離を求めるのに三平方の定理を用いる。以下では単位円のみを取り扱うが、円の半径によらずこの方法から加法定理を得ることができる。
単位円の周上に 2 点 P = (cosp, sinp), Q = (cosq, sinq) を取る。P と Q を結ぶ線分の長さを PQ として、その 2 乗 PQ2 を 2 通りの方法で求めることを考える(右図も参照)。
P と Q の x 座標の差と y 座標の差から、三平方の定理を用いて PQ2 を求める。
次に Q = (cos0, sin0) = (1, 0) となるような座標系を取り、同様に三平方の定理から PQ2 を求める。この座標系に対する操作は、x 軸および y 軸を角度 q だけ回転させる操作に相当するので、P = (cos(p − q), sin(p − q)) となる。従って、
となる。
(1) と (2) の右辺が互いに等しいことから、次の cos に関する加法定理が得られる。
三角関数の他の性質を利用することで、(3) から sin の加法定理なども導くことができる。
不動点
[編集]微積分
[編集]三角関数の微積分は、以下の表のとおりである。ただし、これらの結果には様々な(一見同じには見えない)表示が存在し、この表における表示はいくつかの例であることに注意されたい。
なお、以下の表の C は積分定数、ln(·) は自然対数である。
ただし、gd−1x はグーデルマン関数の逆関数である。 (gd-1x = ln|sec x + tan x|)
三角関数の微分では、次の極限
の成立が基本的である。このとき、sinx の導関数が cosx であることは加法定理から従う(が、後述のようにこれは循環論法であると指摘される)。さらに余角公式 cosx = sin (π/2 − x) から cosx の導関数は −sinx である。すなわち、sinx は微分方程式 y''(x) + y(x) = 0 の特殊解である。また、他の三角関数の導関数も、上の事実から簡単に導ける。
sinx/x の x → 0 における極限
[編集]sinx/x の x → 0 における極限が 1 であることを証明するときに、中心角 x ラジアンの扇形の面積を2つの三角形の面積ではさんだり[9]、弧長を線分の長さではさんだりして[10][11]、いわゆるはさみうちの原理から証明する方法がある。これは一般的な日本の高校の教科書[12][13]にも載っているものであるが、循環論法であるため論理が破綻しているという主張がなされることがある[14][15]。ここで問題となるのは、証明に面積やラジアン、弧長が利用されていることである。例えば面積について言えば、面積は積分によって定義されるものであるとすると、扇形の面積を求めるには三角関数の積分が必要となる。三角関数の積分をするには三角関数の微分ができなければならないが、三角関数を微分するにはもとの極限が必要になる。このことが循環論法と呼ばれているのである。
単位円板の面積が π であることを自明な概念と考えてしまえば循環論法にはならないが、これはいくつかの決められた公理・定義から論理的演繹のみによって証明されたものだけを正しいと考える現代数学の思想とは相反するものである。循環論法を回避する方法の 1 つは、正弦関数と余弦関数を上述のような無限級数で定義するものである(これは三角関数の標準的な定義の 1 つである。また、この無限級数の収束半径は無限大である(すなわち任意の実数や複素数で収束する))。この定義に基づいて
を示すことができる。
しかしながら、このように定義された三角関数が、本来持つべき幾何学的な性質を有しているかどうかは全く明らかなことではない。これを確かめるためには、三角関数の諸公式(周期性やピタゴラスの基本三角関数公式等)を証明し、また円周率は、余弦関数の正の最小の零点(つまり、cosx = 0 となる正の最小の値)の存在を示し、その 2 倍と定義する。すると、 が区間 [0, 2π) から単位円周への(「反時計まわりの」)全単射であることを示すことができる。(連続微分可能な)曲線の長さを積分によって定義すれば、単位円周の長さが 2π であることなどがわかり、上のように定義された三角関数や円周率は、初等幾何での三角関数や円周率の素朴な定義と同じものであることが分かった [注釈 1][16]。
無限乗積展開
[編集]三角関数は以下のように無限乗積として書ける。
部分分数展開
[編集]三角関数は以下のように部分分数に展開される。
逆三角関数
[編集]三角関数の定義域を適当に制限したものの逆関数を逆三角関数(ぎゃくさんかくかんすう、英: inverse trigonometric function)と呼ぶ。逆三角関数は逆関数の記法に則り、元の関数の記号に −1 を右肩に付して表す。たとえば逆正弦関数(ぎゃくせいげんかんすう、英: inverse sine; インバース・サイン)は sin−1x などと表す。arcsin, arccos, arctan などの記法もよく用いられる。数値計算などにおいては、これらの逆関数はさらに asin, acos, atan などと書き表される。
である。逆関数は逆数ではないので注意したい。逆数との混乱を避けるために、逆正弦関数 sin−1x を arcsinx と書く流儀もある。一般に周期関数の逆関数は多価関数になるので、通常は逆三角関数を一価連続なる枝に制限して考えることが多い。たとえば、便宜的に主値と呼ばれる枝を
のように選ぶことが多い。またこのとき、制限があることを強調するために、Sin−1x, Arcsin x のように頭文字を大文字にした表記がよく用いられる。
複素関数として
[編集]exp z, cos z, sin z の級数による定義から、オイラーの公式 exp (iz) = cos z + i sin z を導くことができる。この公式から下記の 2 つの等式
が得られるから、これを連立させて解くことにより、正弦関数・余弦関数の指数関数を用いた表現が可能となる。すなわち、
が成り立つ。この事実により、級数によらずこの等式をもって複素数の正弦・余弦関数の定義とすることもある。また、
が成り立つ。ここで cosh z, sinh z は双曲線関数を表す。この等式は三角関数と双曲線関数の関係式と捉えることもできる。複素数 z を z = x + iy (x, y ∈ R) と表現すると、加法定理より
が成り立つ。
他の三角関数は cscz = 1 / sinz, secz = 1 / cosz, tanz = sinz / cosz, cotz = cosz / sinz によって定義できる。
-
cos(x + iy) の実部のグラフ
-
cos(x + iy) の虚部のグラフ
-
sin(x + iy) の実部のグラフ
-
sin(x + iy) の虚部のグラフ
球面三角法
[編集]球面の三角形 ABC の内角を a, b, c, 各頂点の対辺に関する球の中心角を α, β, γ とするとき、次のような関係が成立する。余弦公式や正弦余弦公式は式の対称性により各記号を入れ替えたものも成立する。
- 正弦公式
- sina : sinb : sinc = sinα : sinβ : sinγ
- 余弦公式
- cosa = −cosb cosc + sinb sinc cosα
- 余弦公式
- cosα = cosβ cosγ + sinβ sinγ cosa
- 正弦余弦公式
- sina cosβ = cosb sinc − sinb cosc cosα
語源
[編集]三角関数の英語の名称の語源について記す。
sineはもとはchord-half(半弦)を意味するサンスクリット jya ̄-ardha起源であり、省略形ji ̄va ̄がアラビア語に音訳されてjibaとなったが、1145年にチェスターのロバートがフワーリズミーのヒサーブ・アル=ジャブル・ワル=ムカーバラをラテン語に翻訳する際に、jaibと混同した事で胸、湾の意味のsinusと翻訳された[17][18]。
tangentは”touching”を意味するラテン語tangens由来で、secantは”cutting”を意味するラテン語secans由来である[19]。
cosine、cotangent、cosecantはそれぞれ接頭辞のco-がついた形であり、co-はcofunctionと共通し、これはcompliment angle(直角三角形の直角でないもう一つの角、余角)に対するsine、tangent、secantという意味である。cosine、cotangentが初めて書かれた形で確認されるのは1620年のエドマンド・ガンターによる”Canon triangulorum”の中である。ラテン語のcosinusとして登場し、これはsinus complementiの略である[20]。
日本語の正弦、余弦に関しては、徐光啓らが編纂した『崇禎暦書』の中で、羅雅谷が1631年に著した『測量全義』の八線のうちに見られる[21][22]。「正」の漢字には、「真向かいの」「主となるもの」という意味がある[23]。
脚注
[編集]注釈
[編集]- ^ 三角関数、円周率、曲線の長さ等の定義の仕方は、複数の流儀がある。
出典
[編集]- ^ a b 山口格「三角関数の研究」『教授学の探究』第7号、北海道大学教育学部教育方法学研究室、1989年3月、1-23頁、ISSN 0288-3511、NAID 120000962860。
- ^ 内藤, 久資 (1999年). “1999年度後期「Fourier 変換とその応用 "403 Forbidden"” (PDF). 2014年10月17日閲覧。[リンク切れ]
- ^ 黒田成俊 2002, pp. 176–183.
- ^ 高木貞治 2010, pp. 202–206.
- ^ 小平邦彦 2003, pp. 95–105.
- ^ 幡谷泰史; 廣澤史彦. “三角関数と円周率” (PDF). 2023年9月20日閲覧。
- ^ 瓜生, 等. “三角関数のさまざまな定義” (PDF). 2014年10月8日閲覧。[リンク切れ]
- ^ Leff, Lawrence S. (2005). PreCalculus the Easy Way (7th ed.). Barron's Educational Series. p. 296. ISBN 0-7641-2892-2
- ^ “面積による不等式からの証明”. 2015年1月20日閲覧。
- ^ “曲線の長さによる不等式からの証明” (PDF). p. 1. 2015年1月20日閲覧。
- ^ 新関章三(元高知大学),矢野 忠(元愛媛大学). “数学・物理通信” (PDF). 2015年1月21日閲覧。
- ^ 大矢雅則、岡部恒治 ほか13名『新編 数学Ⅲ』(改訂版)数研出版株式会社、2010年1月10日、53頁。ISBN 978-4-410-80166-2。 NCID BA89906770。OCLC 676686067。
- ^ 飯高茂、松本幸夫 ほか22名『数学Ⅲ』東京書籍株式会社、2008年2月10日、49頁。ISBN 4-487-15513-4。 NCID BA71854010。OCLC 76931848。ほか
- ^ 川中宣明. “循環論法で証明になっていない” (PDF). p. 1. 2015年1月18日閲覧。
- ^ 杉浦光夫 1980, p. 175.
- ^ 杉浦光夫 1980, pp. 175–185.
- ^ Victor J. Katz (2008), A History of Mathematics, Boston: Addison-Wesley, 3rd. ed., p. 253, sidebar 8.1. “Archived copy”. 2015年4月14日時点のオリジナルよりアーカイブ。2020年12月22日閲覧。
- ^ “The Etymology of “Sine””. Bill Cherowitzo's Home Page, Mathematical Department, University of Colorado at Denver. December 22, 2020閲覧。
- ^ New Oxford American Dictionary
- ^ Roegel, Deni (2010). A reconstruction of Gunter's Canon triangulorum (1620).
- ^ 杜石然「イエズス会士と西洋数学の伝入」『中国言語文化研究』第1巻、佛教大学中国言語文化研究会、2001年7月、1-22頁、CRID 1050287838661758848、ISSN 1346-6305、NAID 110007974156。
- ^ 伊達文治「三角法と対数の教材に関する史的考察」『上越教育大学数学研究』第30巻、上越教育大学数学教室、2015年3月、13-22頁、CRID 1050845763704678656、hdl:10513/00006983、NAID 120005703229。
- ^ 角川新字源 改訂版 角川学芸出版
参考文献
[編集]- Maor, Eli (1998). Trigonometric Delights. Princeton University Press. ISBN 978069105754-5
- 志賀浩二『数の大航海―対数の誕生と広がり』日本評論社、1999年7月。ISBN 978-4-535-78289-1。
- 高瀬正仁『古典的難問に学ぶ微分積分』共立出版、2013年7月。ISBN 978-4-320-11041-0。
- Vinogradov, Ivan Matveyevich (2004-09-10). The Method of Trigonometrical Sums in the Theory of Numbers (revised ed.). Dover. ISBN 978-048643878-8
- 黒川信重、小山信也『多重三角関数論講義』日本評論社、2010年11月8日。ISBN 978-4-535-785557。 ※ 通常の三角関数、ガンマ関数、ゼータ関数などを「多重化」した特殊関数の理論の構築。
- 黒川信重:「現代三角函数論」、岩波書店、ISBN 978-4-00-005327-3 (2013年11月7日). ※ 通常の三角関数、ガンマ関数、ゼータ関数などを「多重化」した特殊関数の理論の構築。
- 杉浦光夫『解析入門I』東京大学出版会〈基礎数学2〉、1980年。ISBN 978-4-13-062005-5。
- 黒田成俊『微分積分』共立出版〈共立講座21世紀の数学 第1巻〉、2002年。ISBN 978-4320015531。
- 高木貞治『定本 解析概論』(改訂第3版)岩波書店、2010年。ISBN 978-4000052092。
- 小平邦彦『解析入門I』(軽装版)岩波書店、2003年。ISBN 978-4000051927。
関連項目
[編集]- 正弦定理
- 余弦定理
- 正接定理
- 球面三角法
- コサイン4乗則
- ベクトルのなす角 - cos 関数を用いて表現される。
- ドット積
- クロス積
- ベッセル関数
- sinc関数
- 指数関数
- 双曲線関数
- オイラーの公式
- 円 - 正円の三角関数との関係
- ベジェ曲線 - 三角関数のベジエ曲線による近似
- テイラー展開 - コンピュータ上での三角関数の実装に使用
- 算数チャチャチャ - 歌詞に三角関数の問題の解き方が含まれる
- 3次元コンピュータグラフィックス
外部リンク
[編集]- 三角比の近似値表
- Weisstein, Eric W. "Trigonometric Functions". mathworld.wolfram.com (英語).
- 江戸時代の三角関数表(これなあに)
- 『三角関数』 - コトバンク