対移動平均比率法
対移動平均比率法(たいいどうへいきんひりつほう、英: ratio-to-moving-average method)は,過去の時系列データから,将来の数値を予測する方法の一つ。需要予測などに用いる。季節変動や曜日変動などの周期性がある場合に有効である。移動平均法の一種であり、比較的単純な方法であるが、実用的な結果を出すことが多い。竹安数博らが1997年に発表した[1]。
原理
[編集]まず、過去のデータから各季節ごとの季節指数を求める。次に、傾向を延長し、それに季節指数を掛けて予測値を得る。
需要などの変動は、傾向変動、循環変動、季節変動、不規則変動などに分解される。
対移動平均比率法では、時系列データ A を傾向変動 (F) と季節変動 (E) の積として捉える。1周期分(例えば1年分)のデータの平均値は、季節変動を除去した値になる。平均値を取る範囲をずらしていくと滑らかな系列(移動平均)B が得られる。そして、原データ A の平均値 B に対する比(対移動平均比率)C を季節ごとに平均した値(季節別平均値)D を正規化して、季節ごとの係数である季節指数 E を知る。
元の時系列データ A を季節指数 E で割れば、季節変動を取り除いた滑らかな系列 F が得られる(F には循環変動と不規則変動だけが残っている)。これを回帰分析して、傾向変動(トレンド)とする(傾向推定)。将来を予測するときは、まず回帰式によって傾向値 F を延長して将来の傾向値 f を推測(外挿)し、次に各季節の季節指数 E を掛けて予測値を得る。
「季節変動」は、必ずしも1年を周期とする季節に限らず、1週を周期とする曜日(曜日変動)でもよい。(竹安ら[2]は、これらを総括して「期間変動」と呼んでいる。そのとき、季節指数を「期間指数」と呼ぶ。)循環の周期が一定している変動ならば、この方法が適用できる。
手法
[編集]ここでは、1年を周期とする「季節変動」をもつ春・夏・秋・冬ごとの季節データを想定して、手法の用語を記述する。過去の数周期分のデータがあるとする。
- 周期性をもつ時系列の原データ A から、1周期分の移動平均の系列 B を計算する。
- 各季節データ A の移動平均 B に対する比率(対移動平均比率)C を計算する。
- 各季節ごとに対移動平均比率 C の平均値(季節別平均値)D を計算する。
- 季節別平均値 D を D 全体の平均値で割って、各季節の季節指数 E を得る。[3]
- 原データ A を季節指数 E で割り、滑らかな傾向値 F を得る。
- 過去の傾向値 F を(最小二乗法によって)回帰分析する。
- 将来の傾向値 f を(回帰式によって)推測する。
- 将来の推測値 f に季節ごとの季節指数 E を掛けた予測値を計算する。
実は、1周期内のデータ数(春・夏・秋・冬の場合は 4)が偶数の場合は移動平均の計算に少し工夫が必要であり、その手法は下の 3.2(#周期が偶数である場合)に示す。
数値例
[編集]まず、1周期内のデータ数が奇数である場合の数値例によって、手法の主要部分の実際を示す。
周期が奇数である場合
[編集]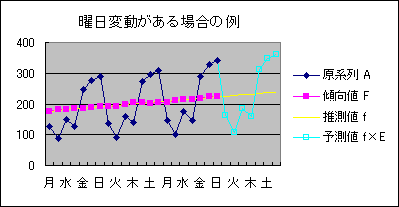
1週を周期とする曜日変動のある場合の計算例とそのグラフを示す。過去の3周期分(先々週から今週まで)の日ごとのデータから、来週1週間分を予測する。
表の下にある段階 6. 傾向の推定 では、傾向値を推定する何らかの手法を用いる。ここでは、直線による回帰分析をしている。
| 段階 | 週 | 月 | 火 | 水 | 木 | 金 | 土 | 日 | 平均 |
|---|---|---|---|---|---|---|---|---|---|
| 0. 原系列 A | 先々週 | 126 | 87 | 149 | 127 | 246 | 276 | 288 | |
| 先週 | 138 | 91 | 160 | 139 | 274 | 297 | 309 | ||
| 今週 | 147 | 101 | 174 | 147 | 289 | 328 | 341 | ||
| 1. 移動平均 B | 先々週 | -- | -- | -- | 185.6 | 187.3 | 187.9 | 189.4 | |
| 先週 | 191.1 | 195.1 | 198.1 | 201.1 | 202.4 | 203.9 | 205.9 | ||
| 今週 | 207.0 | 209.1 | 213.6 | 218.1 | -- | -- | -- | ||
| 2. 対移動平均 比率 C = A/B |
先々週 | -- | -- | -- | 0.684 | 1.313 | 1.469 | 1.521 | |
| 先週 | 0.722 | 0.466 | 0.808 | 0.691 | 1.354 | 1.457 | 1.501 | ||
| 今週 | 0.710 | 0.483 | 0.815 | 0.674 | -- | -- | -- | ||
| 3. 曜日別平均値 | D | 0.716 | 0.475 | 0.811 | 0.683 | 1.334 | 1.463 | 1.511 | 0.999 |
| 4. 曜日指数 | E | 0.717 | 0.475 | 0.812 | 0.684 | 1.335 | 1.464 | 1.512 | 1.000 |
| 5. 傾向値 F = A/E |
先々週 | 175.8 | 183.1 | 183.5 | 185.7 | 184.3 | 188.5 | 190.5 | |
| 先週 | 192.5 | 191.5 | 197.1 | 203.3 | 205.3 | 202.8 | 204.3 | ||
| 今週 | 205.1 | 212.5 | 214.3 | 215.0 | 216.5 | 224.0 | 225.5 | ||
| 7. 推測値 f | 来週 | 225.2 | 227.5 | 229.8 | 232.0 | 234.3 | 236.6 | 238.9 | |
| 8. 予測値 f ×E | 来週 | 161.4 | 108.1 | 186.5 | 158.7 | 312.8 | 346.4 | 361.2 |
6. 傾向の推定 - 傾向値の系列 Fx から最小二乗法によって回帰直線 f = ax + b の係数を求めると、a = 2.29, b = 177.2 を得る。ここで、x はデータの番号とする (x = 0, 1, 2, ..., 20)。
7. 推測値 - 回帰直線 f = 2.29x + 177.2 を用いて、来週の傾向値データ fx を推測する (x = 21, 22, ..., 27)。
周期が偶数である場合
[編集]1周期内のデータ数が偶数である場合には、1. 移動平均 B を計算するときに少し工夫が要る。例えば、単純移動平均をさらに二つずつ平均する方法がある[1]。こうすると移動平均の項数が1つ少なくなるが、各季節の前後のデータを対称かつ均等に扱った平均値が得られる。
| 段階 | 前々年 | 前年 | 今年 | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 季節 | 春 | 夏 | 秋 | 冬 | 春' | 夏' | 秋' | 冬' | 春" | 夏" | 秋" | 冬" | ||||||||||||
| 0. 原系列 A | 126 | 87 | 246 | 288 | 138 | 91 | 274 | 309 | 147 | 101 | 289 | 341 | ||||||||||||
| 4項の単純 移動平均 |
-- | 186.8 | 189.8 | 190.8 | 197.8 | 203.0 | 205.3 | 207.8 | 211.5 | 219.5 | -- | |||||||||||||
| 1. 2項ずつの 移動平均 B |
-- | -- | 188.3 | 190.3 | 194.3 | 200.4 | 204.1 | 206.5 | 209.6 | 215.5 | -- | -- | ||||||||||||
例えば、表の左下隅の値 188.3 は、前々年の春と前年の春'を平均した値と、夏,秋,冬の値との平均になっている。
188.3 = { 186.8 + 189.8 } / 2
= { (春+夏+秋+冬)/4 + (夏+秋+冬+春')/4 } / 2
= { 春 + 2×(夏+秋+冬) + 春'}/4 / 2
= { 春/2 + 夏+秋+冬 + 春'/2}/4 …… 秋を中心として対称
= { (春+春')/2 +夏+秋+冬 }/4
歴史
[編集]対移動平均比率法は、竹安数博が開発し、1997年に『新しい経営数学』[1]で発表した。
竹安らは、2006年にこの手法に関しての特許を取得している[2]。
この節の加筆が望まれています。 |
脚注
[編集]- ^ a b c 佃純誠, 竹安数博, 村松健児『新しい経営工学』中央経済社, 1997, pp. 194-197。ISBN 978-4502408854.
- ^ a b 竹安数博、樋口友紀「データ予測装置、データ予測プログラム」j-platpat, 公開日:2006年12月07日(公開番号:2006331312号)。
- ^ 季節指数 E の平均値は、常に 1 になる。
証明: 季節別平均値を d1, d2, …, dn とし,それらの平均値を μ とする。d1/μ, d2/μ, …, dn/μ の平均値は、(d1/μ + d2/μ + … + dn/μ)/n = (1/μ)(d1 + d2 + … + dn)/n = (1/μ)μ = 1 である。
関連項目
[編集]- 傾向推定
- 季節調整
- 英語版 Seasonality - 節 3 Caluculation に 3.3 ratio-to-moving-average method が記述されている。
外部リンク
[編集]- 特許: 竹安数博、樋口友紀「データ予測装置、データ予測プログラム」公開番号: 特開2006-331312, 公開日: 2006年12月07日。
